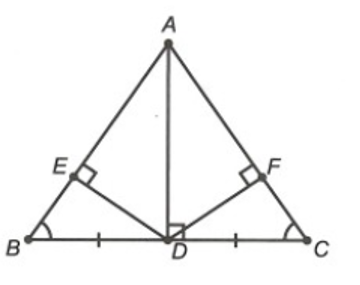
Cho ∆ABC có AB = AC và . Trên cạnh BC, lấy hai điểm D và E sao cho BD = EC. Kẻ DM vuông góc với AB (M ∈ AB) và EN vuông góc với AC (N ∈ AC). Kết luận nào sau đây đúng nhất?
Cho ∆ABC có AB = AC và . Trên cạnh BC, lấy hai điểm D và E sao cho BD = EC. Kẻ DM vuông góc với AB (M ∈ AB) và EN vuông góc với AC (N ∈ AC). Kết luận nào sau đây đúng nhất?
A. ∆AMD = ∆ANE;
B. ∆ABD = ∆ACE;
C. MD = EN;
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Xét ∆ABD và ∆ACE, có:
BD = EC (giả thiết)
(giả thiết)
AB = AC (giả thiết)
Do đó ∆ABD = ∆ACE (c.g.c)
Suy ra và AD = AE (cặp góc và cặp cạnh tương ứng)
Vì vậy phương án B đúng.
Xét ∆AMD và ∆ANE, có:
.
AD = AE (chứng minh trên)
(chứng minh trên)
Do đó ∆AMD = ∆ANE (cạnh huyền – góc nhọn)
Suy ra MD = EN (cặp cạnh tương ứng)
Vì vậy phương án A, C đúng.
Vậy ta chọn phương án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
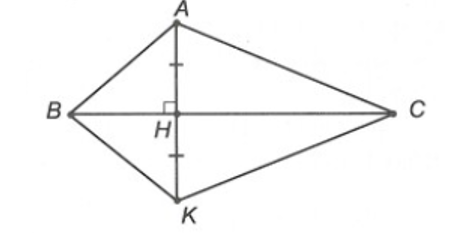
Xét ∆AHB và ∆KHB, có:
HA = HK (giả thiết)
.
BH là cạnh chung.
Do đó ∆AHB = ∆KHB (c.g.c)
Suy ra BA = BK, và (các cặp cạnh và cặp góc tương ứng)
Vì vậy phương án A, C, D đúng, phương án B sai.
Vậy ta chọn phương án B.
Câu 2
A. a – 2; b – 1; c – 3;
B. a – 1; b – 3; c – 2;
C. a – 3; b – 1; c – 2;
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
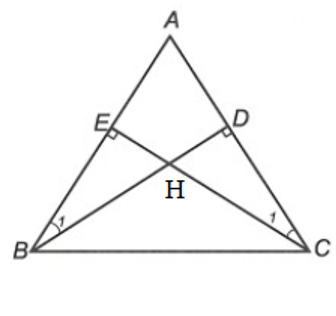
+) Xét ∆ADB và ∆AEC, có:
AB = AC (giả thiết)
.
là góc chung.
Do đó ∆ADB = ∆AEC (cạnh huyền – góc nhọn)
Khi đó a – 3.
+) Vì ∆ADB = ∆AEC nên (cặp góc tương ứng) và AD = BE (cặp cạnh tương ứng)
Ta có: AD + DC = AC, AE + EB = AB
Mà AB = AC, AD = BE nên DC = EB.
Xét ∆HEB và ∆HDC, có:
BE = DC
Suy ra ∆HEB = ∆HDC (g – c – g)
Do đó b – 1.
+) Xét ∆BEC và ∆CDB, có:
BE = DC
BC là cạnh chung
Suy ra ∆BEC = ∆CDB (cạnh góc vuông – cạnh huyền)
Do đó c – 2.
Vậy a – 3, b – 1, c – 2.
Chọn đáp án C.
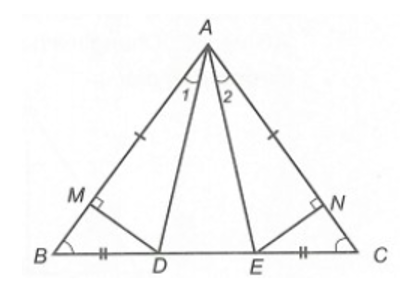
Câu 3
A. ∆AED = ∆AFD;
B. ∆BED = ∆CFD;
C. ∆ADB = ∆ADC;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. BC = 6 cm;
B. BC = 1,5 cm;
C. BC = 9 cm;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. m = 0 và n = 1;
B. m = 2 và n = 1;
C. m = 3 và n = 0;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. AM = DM;
B. ∆ABM = ∆ADM ;
C. ;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.