Phương trình đường tròn đường kính AB với A(1; 3) và B(5; – 1) là A. (x + 3)2 + (y – 1)2 = 8; B. (x + 3)2 + (y + 1)2 = 8; C. (x – 3)2 + (y + 1)2 = 8; D. (x – 3)2 + (y – 1)2 = 8.

Câu hỏi:

14/12/2022 385

Phương trình đường tròn đường kính AB với A(1; 3) và B(5; – 1) là

A. (x + 3)² + (y – 1)² = 8;

B. (x + 3)² + (y + 1)² = 8;

C. (x – 3)² + (y + 1)² = 8;

D. (x – 3)² + (y – 1)² = 8.

Xem lời giải

Câu hỏi trong đề: Đề thi giữa học kì 2 Toán 7 KNTT có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: D

Đường tròn đường kính AB có tâm là trung điểm I của AB và có bán kính bằng nửa độ dài đoạn AB.

Ta có \(\overrightarrow {AB} = \left( {4;\,\, - 4} \right)\), suy ra \(AB = \sqrt {{4^2} + {{\left( { - 4} \right)}^2}} = 4\sqrt 2 \).

Suy ra bán kính đường tròn là \(R = \frac{{AB}}{2} = 2\sqrt 2 \).

Tọa độ tâm là \(\left\{ \begin{array}{l}{x_I} = \frac{{1 + 5}}{2} = 3\\{y_I} = \frac{{3 + \left( { - 1} \right)}}{2} = 1\end{array} \right.\). Suy ra I(3; 1).

Phương trình đường tròn cần lập là: (x – 3)² + (y – 1)² = 8.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là

A. \(2\sqrt {13} \);

B. \(\frac{{28}}{{\sqrt {13} }}\);

C. 26;

D. \(\frac{{\sqrt {13} }}{2}\).

Lời giải

Đáp án đúng là: A

Khoảng cách từ điểm M(5; – 1) đến d: 3x + 2y + 13 = 0 là

\(d\left( {M,\,\,d} \right) = \frac{{\left| {3 \cdot 5 + 2 \cdot \left( { - 1} \right) + 13} \right|}}{{\sqrt {{3^2} + {2^2}} }} = \frac{{26}}{{\sqrt {13} }} = 2\sqrt {13} \).

Câu 2

Viết phương trình tổng quát của đường thẳng

đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;

Xem đáp án

Lời giải

Gọi đường thẳng cần lập là d.

Vectơ pháp tuyến của đường thẳng 3x + 5y – 2 = 0 cũng là một vectơ pháp tuyến của đường thẳng d nên phương trình đường thẳng d có dạng 3x + 5y + c = 0 (c ≠ – 2).

Vì d đi qua điểm M(– 1; – 4) nên 3 . (– 1) + 5 . (– 4) + c = 0. Suy ra c = 23 (t/m).

Vậy phương trình tổng quát của đường thẳng d là 3x + 5y + 23 = 0.

Câu 3

Cho phương trình \(\sqrt { - {x^2} + 4x - 3} = \sqrt {2m + 3x - {x^2}} \) (1). Để phương trình (1) có nghiệm thì m ∈ [a; b]. Giá trị a² + b² bằng

A. 2

B. 4

C. 1

D. 3

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Viết phương trình tổng quát của đường thẳng đi qua N(1; 1) và vuông góc với đường thẳng 2x + 3y + 7 = 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

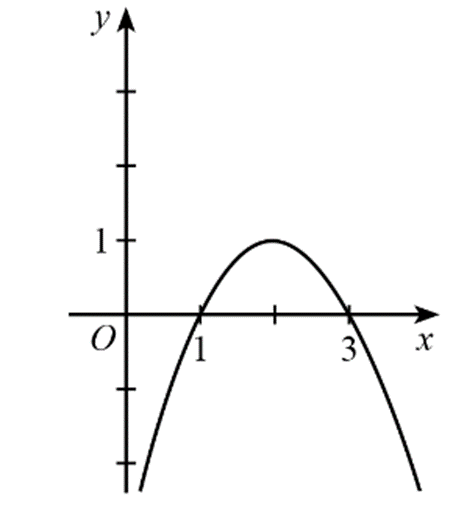
Câu 5

Cho hàm số y = f(x) có đồ thị như hình dưới đây.

Trong các phát biểu sau, phát biểu nào sai?

A. f(x) < 0 khi và chỉ khi x ∈ (1; 3);

B. f(x) ≤ 0 khi và chỉ khi x ∈ (– ∞; 1] ∪ [3; + ∞);

C. f(x) > 0 khi và chỉ khi x ∈ (1; 3);

D. f(x) ≥ 0 khi và chỉ khi x ∈ [1; 3].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho đường thẳng d có phương trình tổng quát: x + 2y – 3 = 0. Phương trình tham số của đường thẳng d là

A. \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 - t\end{array} \right.\);

B. \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 + t\end{array} \right.\);

C. \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 1 - t\end{array} \right.\);

D. \(\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\end{array} \right.\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong các phát biểu sau, phát biểu nào là đúng?

A. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập nghiệm của phương trình ax² + bx + c = dx² + ex + f;

B. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập nghiệm của phương trình (ax² + bx + c)² = (dx² + ex + f)²;

C. Mọi nghiệm của phương trình ax² + bx + c = dx² + ex + f đều là nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \];

D. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập hợp các nghiệm của phương trình ax² + bx + c = dx² + ex + f thỏa mãn bất phương trình ax² + bx + c ≥ 0 (hoặc dx² + ex + f ≥ 0).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Phương trình đường tròn đường kính AB với A(1; 3) và B(5; – 1) là

Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là

Viết phương trình tổng quát của đường thẳng đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;

Cho phương trình \(\sqrt { - {x^2} + 4x - 3} = \sqrt {2m + 3x - {x^2}} \) (1). Để phương trình (1) có nghiệm thì m ∈ [a; b]. Giá trị a2 + b2 bằng

Viết phương trình tổng quát của đường thẳng đi qua N(1; 1) và vuông góc với đường thẳng 2x + 3y + 7 = 0.

Cho hàm số y = f(x) có đồ thị như hình dưới đây. Trong các phát biểu sau, phát biểu nào sai?

Cho đường thẳng d có phương trình tổng quát: x + 2y – 3 = 0. Phương trình tham số của đường thẳng d là

Trong các phát biểu sau, phát biểu nào là đúng?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Viết phương trình tổng quát của đường thẳng

đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;

Cho phương trình \(\sqrt { - {x^2} + 4x - 3} = \sqrt {2m + 3x - {x^2}} \) (1). Để phương trình (1) có nghiệm thì m ∈ [a; b]. Giá trị a² + b² bằng

Cho hàm số y = f(x) có đồ thị như hình dưới đây.

Trong các phát biểu sau, phát biểu nào sai?