Giả sử x và y là hai đại lượng tỉ lệ thuận, x1; x2 là hai giá trị khác nhau của x và y1; y2 là hai giá trị tương ứng của y. Biết y1 – x1 = 7 và x2 = – 4; y2 = 3, giá trị của x1; y1 là
Giả sử x và y là hai đại lượng tỉ lệ thuận, x1; x2 là hai giá trị khác nhau của x và y1; y2 là hai giá trị tương ứng của y. Biết y1 – x1 = 7 và x2 = – 4; y2 = 3, giá trị của x1; y1 là
A. x1 = –28; y1 = 21;
B. x1 = –3; y1 = 4;
C. x1 = –4; y1 = 3;
D. x1 = 4; y1 = –3.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Áp dụng tính chất tỉ lệ thuận và tính chất dãy tỉ số bằng nhau
Vì x và y là hai đại lượng tỉ lệ thuận nên \[\frac{{{x_1}}}{{{x_2}}} = \frac{{{y_1}}}{{{y_2}}}\]
Suy ra \[\frac{{{x_1}}}{{ - 4}} = \frac{{{y_1}}}{3} = \frac{{{y_1} - {x_1}}}{{3 - \left( { - 4} \right)}} = \frac{7}{7} = 1\]
Nên x1 = 1.(–4) = –4; y1 = 1.3 = 3.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
M(x) = P(x) + Q(x).
M(x) = (5x5 – 4x2 – 7x + 15) + (–5x5 + 4x2 + 3x – 7)
= 5x5 – 4x2 – 7x + 15 – 5x5 + 4x2 + 3x – 7
= –4x + 8.
Ta có M(x) = 0
Suy ra –4x + 8 = 0
x = 2.
Vậy đa thức M(x) có nghiệm là x = 2.
Lời giải
Ta thực hiện đặt tính chia đa thức như sau:
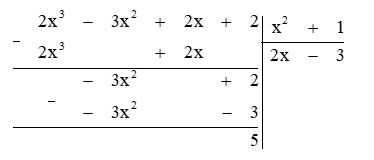
Để đa thức A(x) = 2x3 – 3x2 + 2x + 2 chia hết cho đa thức B(x) = x2 + 1 thì 5 ⁝ (x2 + 1)
Hay (x2 + 1) ∈ Ư(5) = {–1; 1; –5; 5}.
Mà x2 + 1 ≥ 1 với mọi số nguyên x.
Do đó (x2 + 1) ∈ {1; 5}.
• Với x2 + 1 = 1 suy ra x = 0 (thỏa mãn x là số nguyên)
• Với x2 + 1 = 5
Suy ra x2 = 4
Do đó x = 2 (thỏa mãn) hoặc x = –2 (thỏa mãn)
Vậy có 3 giá trị của x thỏa mãn đề bài là x ∈ {0; –2; 2}.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. AB + BC < AC;
B. AC – BC > AB;
C. AB + BC > AC;
D. AB + BC = AC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Biến cố chắc chắn luôn xảy ra;
B. Biến cố không thể không bao giờ xảy ra;
C. Xác suất của biến cố ngẫu nhiên bằng 1;
D. Biến cố có khả năng xảy ra cao hơn sẽ có xác suất lớn hơn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập