Câu hỏi:
19/12/2022 3,722
Cho tam giác ABC với hai đường trung tuyến BM và CN cắt nhau tại G. Kết luận nào sau đây là sai?
Cho tam giác ABC với hai đường trung tuyến BM và CN cắt nhau tại G. Kết luận nào sau đây là sai?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
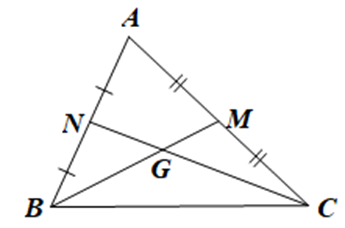
Cho DABC có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm của DABC.
Khi đó \(CG = \frac{2}{3}CN\); \(GN = \frac{1}{2}GC\); \(GM = \frac{1}{3}BM\); \(GB = 2GM\). Do đó C sai.
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới)
Đã bán 230
₫ 235.000
₫ 120.000
Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới)
Đã bán 361
₫ 245.000
₫ 126.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
Tìm nghiệm của đa thức M(x) biết M(x) = P(x) + Q(x).
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
Tìm nghiệm của đa thức M(x) biết M(x) = P(x) + Q(x).
Xem đáp án »
11/07/2024
7,387
Câu 2:
Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:
A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.
B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.
C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.
D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.
Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:
A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.
B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.
C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.
D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.
Xem đáp án »
11/07/2024
7,222
Câu 3:
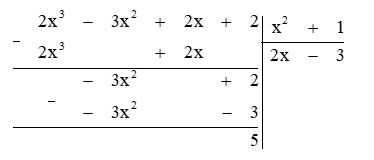
Tìm số nguyên x để đa thức A(x) = 2x3 – 3x2 + 2x + 2 chia hết cho đa thức B(x) = x2 + 1.
Tìm số nguyên x để đa thức A(x) = 2x3 – 3x2 + 2x + 2 chia hết cho đa thức B(x) = x2 + 1.
Xem đáp án »
11/07/2024
6,364
Câu 6:
Số đo ba góc của một tam giác tỉ lệ với 4; 6; 8. Tính số đo mỗi góc của tam giác đó.
Số đo ba góc của một tam giác tỉ lệ với 4; 6; 8. Tính số đo mỗi góc của tam giác đó.
Xem đáp án »
11/07/2024
4,667
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 4
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận