Câu hỏi:

13/07/2024 2,561

Cho nửa đường tròn tâm O, đường kính $A B = 2 R$ . Trên nửa mặt phẳng có bờ là AB chứa nửa đường tròn, vẽ tiếp tuyến Ax, By. Từ điểm M tùy ý thuộc đường tròn (M khác A, B) vẽ tiếp tuyến tại M cắt Ax, By lần lượt tại C, D. Gọi E là giao điểm của CO và AM, F là giao điểm của DO và BM.

Chứng minh 4 điểm A, C, M, O cùng thuộc một đường tròn.

Xem lời giải

Câu hỏi trong đề: Bộ 15 đề kiểm tra học kì 1 Toán 9 năm 2022-2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

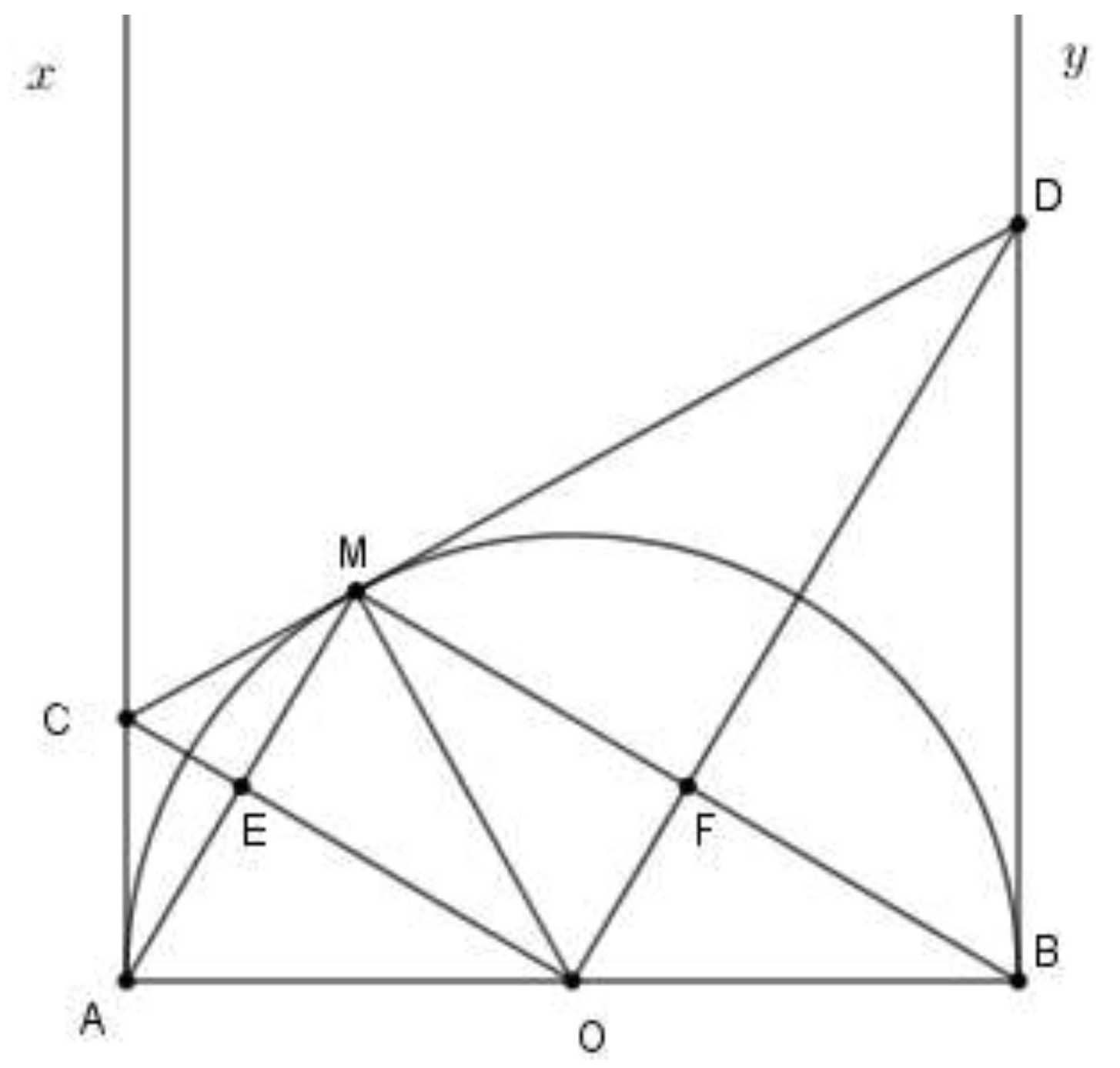
Media VietJack

Vì tam giác $Δ O A C$ vuông tại A nên nó nội tiếp đường tròn đường kính CO (1)

Lại có $Δ O M C$ vuông tại M (do MC là tiếp tuyến tại M) nên nó nội tiếp đường tròn đường kính CO (2)

Từ (1) và (2) $\Rightarrow A, C, M, O$ cùng thuộc một đường tròn có đường kính CO (đpcm).

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một cột cờ vuông góc với mặt đất có bóng dài 12m, tia nắng của mặt trời tạo với mặt đất một góc là $35 °$ (hình vẽ bên). Tính chiều cao của cột cờ.

Xem đáp án

Lời giải

Ta đưa về bài toán. Cho tam giác ABC vuông tại A có , $A C = 12 m$ $∠ B C A = 35 °$ . Tính AB.

Chiều cao cột cờ là AB.

Do $Δ A B C$ vuông tại A nên ta có:

$\begin{matrix} A B = A C . \tan C \\ = 12. \tan 35 ° \\ = 8, 402 (m) \end{matrix}$

Câu 2

Cho hàm số bậc nhất $y = (m + 1) x + 2$ có đồ thị $(d)$ (m là tham số và $m \neq - 1$ )

Xác định m để (d) cắt hai trục Ox, Oy tại A và B sao cho tam giác AOB có diện tích bằng 2 (đơn vị diện tích).

Xem đáp án

Lời giải

Do $m \neq - 1$ nên không mất tính tổng quát ta giả sử (d) cắt Ox và Oy như hình vẽ

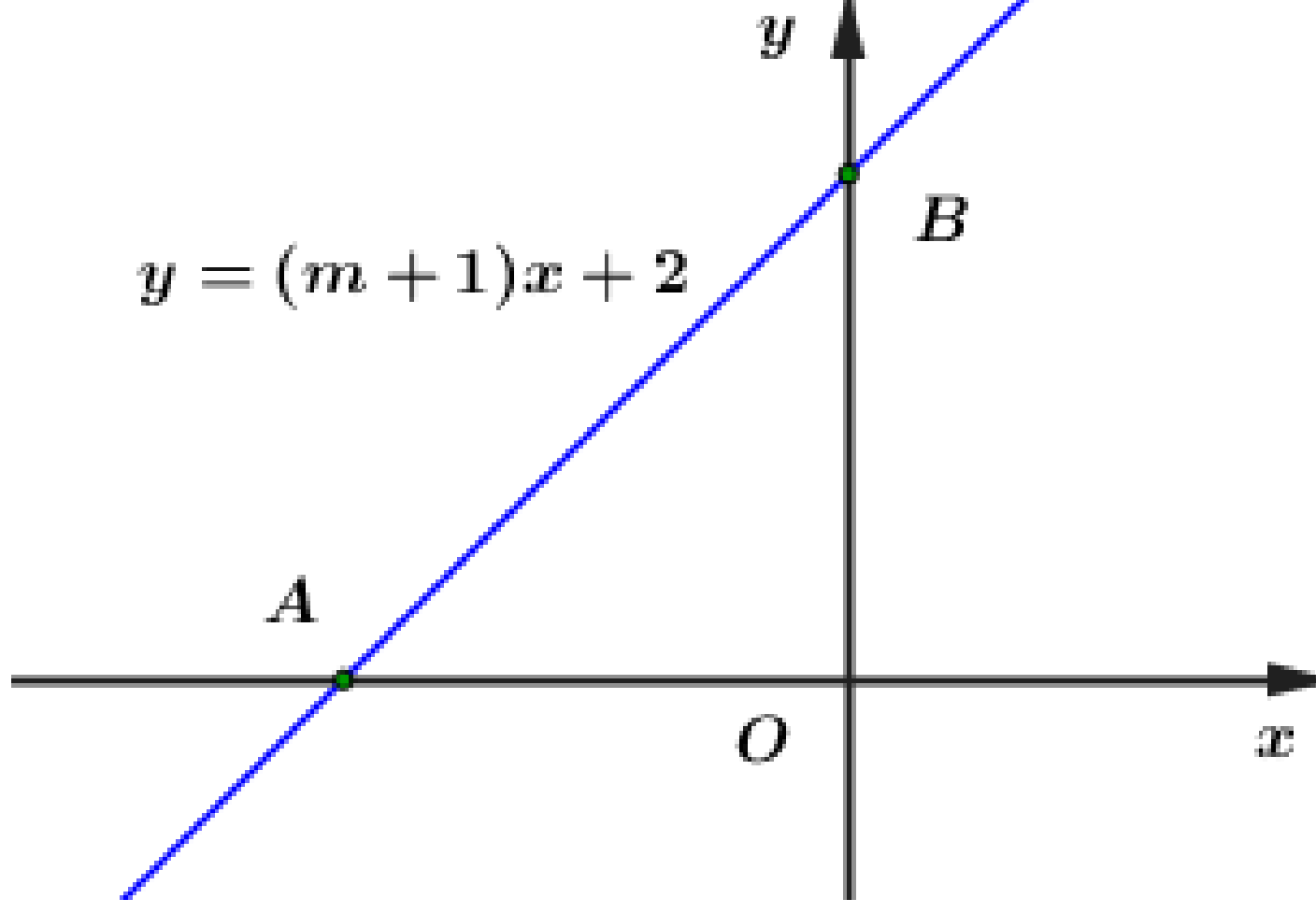
Media VietJack

Vì A là giao điểm của $(d)$ với Ox nên $A (x; 0) \Rightarrow (m + 1) x + 2 = 0 \Rightarrow x = - \frac{2}{m + 1}$

Suy ra $A (- \frac{2}{m + 1}; 0) \Rightarrow O A = \frac{2}{|m + 1|}$

Vì B là giao điểm của $(d)$ với Oy nên $B (0; y) \Rightarrow (m + 1) .0 + 2 = y \Rightarrow y = 2$

Suy ra $B (0; 2) \Rightarrow O B = 2$

Vì $Δ O A B$ vuông tại O.

Khi đó: $S_{Δ O A B} = \frac{1}{2} O A . O B = \frac{1}{2} . \frac{2}{|m + 1|} .2 = \frac{2}{|m + 1|}$

Mà $S_{Δ O A B} = 2 \Leftrightarrow |m + 1| = 1 \Leftrightarrow [\begin{array}{l} m + 1 = 1 \\ m + 1 = - 1 \end{array} \Leftrightarrow [\begin{array}{l} m = 0 \\ m = - 2 \end{array}$ (thỏa mãn $m \neq - 1$ )

Vậy $m = 0$ hoặc $m = - 2$ thỏa mãn yêu cầu bài toán.

Câu 3

Cho nửa đường tròn tâm O, đường kính $A B = 2 R$ . Trên nửa mặt phẳng có bờ là AB chứa nửa đường tròn, vẽ tiếp tuyến Ax, By. Từ điểm M tùy ý thuộc đường tròn (M khác A, B) vẽ tiếp tuyến tại M cắt Ax, By lần lượt tại C, D. Gọi E là giao điểm của CO và AM, F là giao điểm của DO và BM.
Tìm vị trí của M trên nửa đường tròn sao cho diện tích tứ giác ABDC nhỏ nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho các biểu thức $A = \frac{\sqrt{x}}{\sqrt{x} + 2}$ ; $B = \frac{x}{x - 4} - \frac{1}{2 - \sqrt{x}} + \frac{1}{\sqrt{x} + 2}$ (với $x \geq 0; x \neq 4$ )
Tìm các giá trị nguyên của x để biểu thức P=A.B có giá trị là số nguyên

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho các biểu thức $A = \frac{\sqrt{x}}{\sqrt{x} + 2}$ ; $B = \frac{x}{x - 4} - \frac{1}{2 - \sqrt{x}} + \frac{1}{\sqrt{x} + 2}$ (với $x \geq 0; x \neq 4$ )

Tính giá trị của biểu thức A khi x=36.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số bậc nhất $y = (m + 1) x + 2$ có đồ thị $(d)$ (m là tham số và $m \neq - 1$ )

Xác định m để đường thẳng (d) song song với đường thẳng y=2x+1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Một cột cờ vuông góc với mặt đất có bóng dài 12m, tia nắng của mặt trời tạo với mặt đất một góc là 35° (hình vẽ bên). Tính chiều cao của cột cờ.

Cho hàm số bậc nhất y=m+1x+2 có đồ thị d (m là tham số và m≠−1 ) Xác định m để (d) cắt hai trục Ox, Oy tại A và B sao cho tam giác AOB có diện tích bằng 2 (đơn vị diện tích).

Cho các biểu thức A=xx+2 ;B=xx−4−12−x+1x+2 (với x≥0; x≠4 ) Tìm các giá trị nguyên của x để biểu thức P=A.B có giá trị là số nguyên

Cho các biểu thức A=xx+2 ;B=xx−4−12−x+1x+2 (với x≥0; x≠4 ) Tính giá trị của biểu thức A khi x=36.

Cho hàm số bậc nhất y=m+1x+2 có đồ thị d (m là tham số và m≠−1 ) Xác định m để đường thẳng (d) song song với đường thẳng y=2x+1.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Một cột cờ vuông góc với mặt đất có bóng dài 12m, tia nắng của mặt trời tạo với mặt đất một góc là $35 °$ (hình vẽ bên). Tính chiều cao của cột cờ.

Cho hàm số bậc nhất $y = (m + 1) x + 2$ có đồ thị $(d)$ (m là tham số và $m \neq - 1$ )

Xác định m để (d) cắt hai trục Ox, Oy tại A và B sao cho tam giác AOB có diện tích bằng 2 (đơn vị diện tích).

Cho các biểu thức $A = \frac{\sqrt{x}}{\sqrt{x} + 2}$ ; $B = \frac{x}{x - 4} - \frac{1}{2 - \sqrt{x}} + \frac{1}{\sqrt{x} + 2}$ (với $x \geq 0; x \neq 4$ )
Tìm các giá trị nguyên của x để biểu thức P=A.B có giá trị là số nguyên

Cho các biểu thức $A = \frac{\sqrt{x}}{\sqrt{x} + 2}$ ; $B = \frac{x}{x - 4} - \frac{1}{2 - \sqrt{x}} + \frac{1}{\sqrt{x} + 2}$ (với $x \geq 0; x \neq 4$ )

Tính giá trị của biểu thức A khi x=36.

Cho hàm số bậc nhất $y = (m + 1) x + 2$ có đồ thị $(d)$ (m là tham số và $m \neq - 1$ )

Xác định m để đường thẳng (d) song song với đường thẳng y=2x+1.