Câu hỏi:
13/07/2024 2,409
Cho tam giác ABC có các góc đều nhọn và có ba đường cao là AD, BE, CF cắt nhau tại H.
a) Chứng minh các tứ giác BCEF, AEHF là các tứ giác nội tiếp
Cho tam giác ABC có các góc đều nhọn và có ba đường cao là AD, BE, CF cắt nhau tại H.
a) Chứng minh các tứ giác BCEF, AEHF là các tứ giác nội tiếp
Câu hỏi trong đề: Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
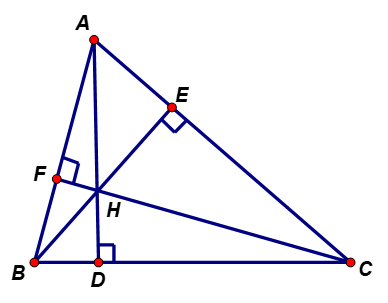
a) Ta có: (Vì BE, CF là đường cao của tam giác ABC)
Vậy tứ giác BCEF nội tiếp được đường tròn đường kính BC
Ta có: (Vì BE, CF là đường cao của tam giác ABC)
Vậy tứ giác AEHF nội tiếp được đường tròn đường kính AHHot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
c) Tứ giác CEHD nội tiếp đường tròn đường kính CH
( 2 góc nội tiếp chắn cùng cung HE)
Tứ giác BCEF nội tiếp đường tròn đường kính BC
( 2 góc nội tiếp chắn cùng cung FE)
Tứ giác BDHF nội tiếp đường tròn đường kính BH
( 2 góc nội tiếp chắn cùng cung FH)
Vậy
Suy ra DH là đường phân giác của góc EDF trong tam giác DEF.
Chứng minh tương tự ta có:
EH là đường phân giác của góc DEF trong tam giác DEF.
Vậy H là tâm của đường tròn nội tiếp của tam giác DEF.Lời giải
Gọi lãi suất cho vay là X (% ; X > 0)
Tiền lãi sau một năm là: 10 000 000. X % = 100 000. X (đồng)
Sau một năm cả vốn lẫn lãi là: (10 000 000 + 100 000. X) (đồng)
Tiền lãi riêng năm thứ hai phải chịu là : (10 000 000 + 100 000. X).X % = 100 000.X + 1000.X2
Số tiền sau 2 năm bác Thanh phải trả cho ngân hàng là :
(10 000 000 + 100 000 X) + 100 000 X + 1000.X2 (đồng)
Theo đầu bài ta có phương trình:
10 000.000 + 200 000 X + 1 000X2 = 11664000
hay X2 + 200 X – 1664 = 0
Giải phương trình ta được:
X = 8 (nhận) hay X = - 208 (loại)
Vậy lãi suất cho vay là 8 % một nămLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 1. Phương trình quy về phương trình bậc nhất một ẩn có đáp án
Nhắn tin Zalo