Câu hỏi trong đề: Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 !!
Quảng cáo
Trả lời:
c) Tứ giác CEHD nội tiếp đường tròn đường kính CH
( 2 góc nội tiếp chắn cùng cung HE)
Tứ giác BCEF nội tiếp đường tròn đường kính BC
( 2 góc nội tiếp chắn cùng cung FE)
Tứ giác BDHF nội tiếp đường tròn đường kính BH
( 2 góc nội tiếp chắn cùng cung FH)
Vậy
Suy ra DH là đường phân giác của góc EDF trong tam giác DEF.
Chứng minh tương tự ta có:
EH là đường phân giác của góc DEF trong tam giác DEF.
Vậy H là tâm của đường tròn nội tiếp của tam giác DEF.Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi lãi suất cho vay là X (% ; X > 0)
Tiền lãi sau một năm là: 10 000 000. X % = 100 000. X (đồng)
Sau một năm cả vốn lẫn lãi là: (10 000 000 + 100 000. X) (đồng)
Tiền lãi riêng năm thứ hai phải chịu là : (10 000 000 + 100 000. X).X % = 100 000.X + 1000.X2
Số tiền sau 2 năm bác Thanh phải trả cho ngân hàng là :
(10 000 000 + 100 000 X) + 100 000 X + 1000.X2 (đồng)
Theo đầu bài ta có phương trình:
10 000.000 + 200 000 X + 1 000X2 = 11664000
hay X2 + 200 X – 1664 = 0
Giải phương trình ta được:
X = 8 (nhận) hay X = - 208 (loại)
Vậy lãi suất cho vay là 8 % một nămLời giải
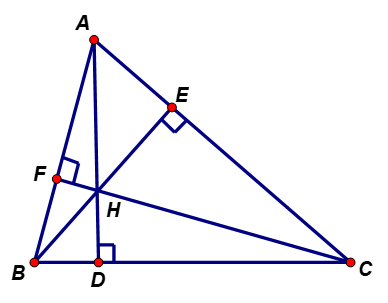
a) Ta có: (Vì BE, CF là đường cao của tam giác ABC)
Vậy tứ giác BCEF nội tiếp được đường tròn đường kính BC
Ta có: (Vì BE, CF là đường cao của tam giác ABC)
Vậy tứ giác AEHF nội tiếp được đường tròn đường kính AHLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.