Cho tam giác ABC vuông tại A có AB = 3cm; AC = 4cm, đường cao AH.
a) Tính BC,AH;
b) Vẽ (A:AH), vẽ HI vuông góc với AC, HI cắt (A) tại M. Chứng minh: CM là tiếp tuyến của (A);
c) Vẽ đường kính MG của (A). Chứng minh BG là tiếp tuyến của (A)
Cho tam giác ABC vuông tại A có AB = 3cm; AC = 4cm, đường cao AH.
a) Tính BC,AH;
b) Vẽ (A:AH), vẽ HI vuông góc với AC, HI cắt (A) tại M. Chứng minh: CM là tiếp tuyến của (A);
c) Vẽ đường kính MG của (A). Chứng minh BG là tiếp tuyến của (A)
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
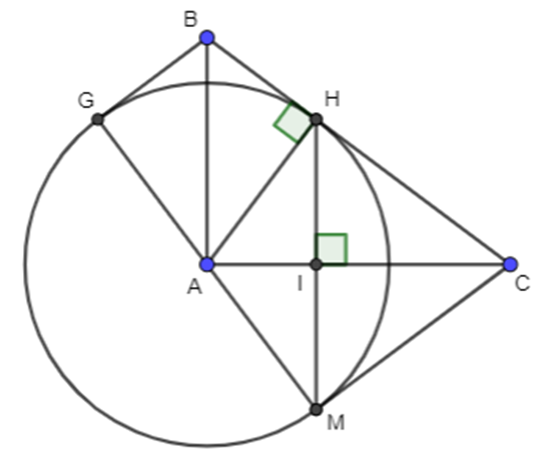
a) Áp dụng định lí Pytago vào \[\Delta ABC\] vuông tại A, ta được:
\[B{C^2} = A{B^2} + A{C^2}\]
\[ \Leftrightarrow B{C^2} = {3^2} + {4^2} = 25\]
hay BC = 5(cm)
Xét \[\Delta ABC\] vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\[AH \cdot BC = AB \cdot AC\]
\[ \Leftrightarrow AH \cdot 5 = 3 \cdot 4 = 12\]
hay AH = 2,4(cm)
Vậy: BC = 5cm; AH = 2,4cm
b) Xét (A) có
AI là một phần đường kính
MH là dây
\[AI \bot MH\] tại I(gt)
Do đó: I là trung điểm của MH(Định lí đường kính vuông góc với dây)
Xét \[\Delta CMI\] vuông tại I và \[\Delta CHI\] vuông tại I có
CI chung
IM = IH(I là trung điểm của MH)
Do đó:\[\Delta CMI = \Delta CHI\] (hai cạnh góc vuông)
Suy ra: CM = CH(hai cạnh tương ứng)
Xét \[\Delta CMA\] và \[\Delta CHA\] có
CM = CH(cmt)
CA chung
AM = AH( = R)
Do đó: \[\Delta CMA = \Delta CHA\left( {c - c - c} \right)\]
Suy ra:\[\widehat {CMA} = \widehat {CHA}\] (Hai góc tương ứng)
mà\[\widehat {CHA} = {90^0}\] (gt)
nên \[\widehat {CMA} = {90^0}\]
hay CM là tiếp tuyến của (A)
251. có bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau và là số lẻ
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
O là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 0 = 0
1 là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 1 = 1
Lời giải
Hai góc tương ứng là hai góc của hai tam giác khác nhau.
Hai góc đó bằng nhau và nằm trong hai tam giác bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[{\rm{3}}\overrightarrow {{\rm{IM}}} {\rm{ + 4}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
B. \[\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + 4}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
C. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
D. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + }}\overrightarrow {{\rm{IN}}} {\rm{ + 3}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập