Cho đường tròn tâm O bán kính R và một đường thẳng d cố định không giao nhau. Hạ OH vuông góc với d. M là một điểm tùy ý trên d (M không trùng với H). Từ M kẻ hai tiếp tuyến MP và MQ với đường tròn (O; R) (P, Q là các tiếp điểm và tia MQ nằm giữa hai tia MH và MO). Dây cung PQ cắt OH và OM lần lượt tại I và K.
1) Chứng minh rằng tứ giác OMHQ nội tiếp.
2) Chứng minh rằng \[\widehat {OMH} = \widehat {OIP}\]
3) Chứng minh rằng khi M di chuyển trên đường thẳng d thì điểm I luôn cố định.
4) Biết \[OH = R\sqrt 2 \], tính IP . IQ.
Cho đường tròn tâm O bán kính R và một đường thẳng d cố định không giao nhau. Hạ OH vuông góc với d. M là một điểm tùy ý trên d (M không trùng với H). Từ M kẻ hai tiếp tuyến MP và MQ với đường tròn (O; R) (P, Q là các tiếp điểm và tia MQ nằm giữa hai tia MH và MO). Dây cung PQ cắt OH và OM lần lượt tại I và K.
1) Chứng minh rằng tứ giác OMHQ nội tiếp.
2) Chứng minh rằng \[\widehat {OMH} = \widehat {OIP}\]
3) Chứng minh rằng khi M di chuyển trên đường thẳng d thì điểm I luôn cố định.
4) Biết \[OH = R\sqrt 2 \], tính IP . IQ.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
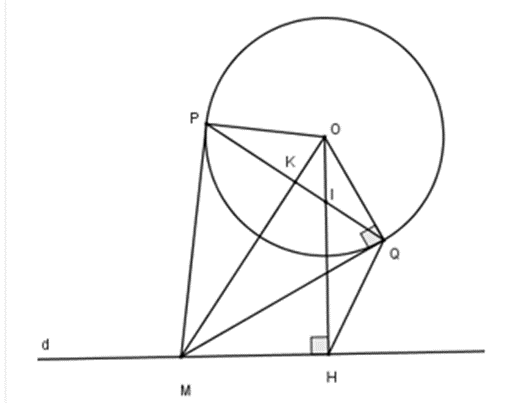
1) Xét tứ giác OMHQ có \[\widehat {OQM} = {90^0}\] (MQ là tiếp tuyến của (O))
\[\widehat {OHM} = {90^0}\] (\[OH \bot d\])
Vậy tứ giác OMHQ nội tiếp (Tứ giác có hai góc nội tiếp bằng nhau)
2) Ta có: \[\widehat {OMH} + \widehat {MOH} = {90^0}\] (tổng hai góc nhọn trong tam giác vuông OMH)
Ta có OP = OQ = R, MP = MQ (tính chất hai tiếp tuyến cắt nhau)
→ OM là trung trực của PQ \[ \to OM \bot PQ\]
\[ \to \widehat {OIP} + \widehat {MOH} = {90^0}\] (tổng hai góc nhọn trong tam giác vuông OIK)
Vậy \[\widehat {OMH} = \widehat {OIP}\] (cùng phụ với \[\widehat {MOH}\])
3) Xét hai tam giác OIK và OMH có \[\widehat {OMH} = \widehat {OIP}\] (cmt), \[\widehat {OHM} = \widehat {OKI} = {90^0}\]
Suy ra \[\Delta OIK \sim \Delta OMH\] (g.g)
\( \to \frac{{OI}}{{OM}} = \frac{{OK}}{{OH}} \to OI = \frac{{OK.OM}}{{OH}}\)
Áp dụng hệ thức lượng trong tam giác vuông OQM có \({R^2} = O{Q^2} = OK.OM\)
\( \to OI = \frac{{{R^2}}}{{OH}}\)
Vì d cố định nên OH không đổi, R luôn không đổi nên OI không đổi. Mà \[I \in OH\] cố định nên I cố định.
4) Xét tứ giác OPMQ có:
\[\widehat {OPM} + \widehat {OQM} = {180^0} \to \] Tứ giác OPMQ nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)) \[ \to \widehat {OPI} = \widehat {OMQ}\](hai góc nội tiếp cùng chắn cung OQ)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
O là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 0 = 0
1 là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 1 = 1
Lời giải
Hai góc tương ứng là hai góc của hai tam giác khác nhau.
Hai góc đó bằng nhau và nằm trong hai tam giác bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[{\rm{3}}\overrightarrow {{\rm{IM}}} {\rm{ + 4}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
B. \[\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + 4}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
C. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
D. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + }}\overrightarrow {{\rm{IN}}} {\rm{ + 3}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập