Cho hình thang cân abcd (ab // cd) có 2 đường chéo vuông góc. Biết đường cao AH = a. Hãy tính tổng 2 đáy theo a
Cho hình thang cân abcd (ab // cd) có 2 đường chéo vuông góc. Biết đường cao AH = a. Hãy tính tổng 2 đáy theo a
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
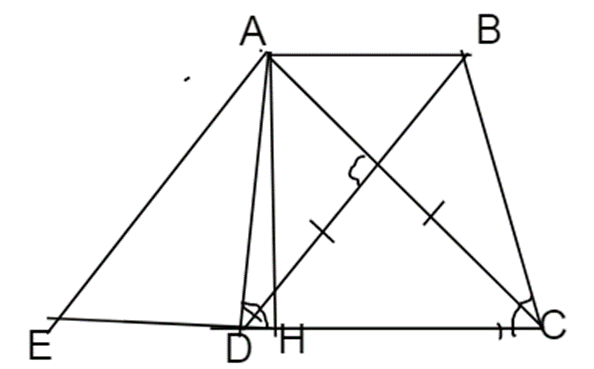
*Cách vẽ:
Nhận xét : Thang cân → 2 đường chéo bằng nhau. Gọi O là giao của 2 đường chéo,
hai đường chéo vuông góc → \(\Delta OCD\)vuông cân đỉnh O.
Vẽ: Vẽ tam giác vuông cân COD, trên tia đối của tia OC lấy A, trên tia đối của tia
OD lấy B sao cho OA = OB (< OC nếu AB là đáy nhỏ) → ABCD là thang cân đáy nhỏ AB, đáy lớn CD và có 2 đường chéo vuông góc.
*Tính AB + CD:
Từ A và B hạ AH và BK vuông góc CD, H, K thuộc CD. Do ABCD là thang cân đáy AB, CD
→ DH = CK và AB = HK
→ AB + CD = AB + DH + HK + KC = HK + CK + HK + KC = 2HC
\(\Delta OCD\) vuông cân đỉnh O \( \to \widehat {OCD} = {45^0} \to \widehat {ACD} = {45^0}\) lại có \(\Delta AHC\) vuông tại H, \(\widehat {ACD} = {45^0} \to \)vuông cân → HC = AH = h
→ tổng 2 đáy AB + CD = 2h
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
O là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 0 = 0
1 là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 1 = 1
Lời giải
Hai góc tương ứng là hai góc của hai tam giác khác nhau.
Hai góc đó bằng nhau và nằm trong hai tam giác bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[{\rm{3}}\overrightarrow {{\rm{IM}}} {\rm{ + 4}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
B. \[\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + 4}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
C. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
D. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + }}\overrightarrow {{\rm{IN}}} {\rm{ + 3}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập