Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị \[\overrightarrow {{\rm{AM}}} \] theo \[\overrightarrow {{\rm{AB}}} \] và \[\overrightarrow {{\rm{AD}}} {\rm{.}}\]

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có hình vẽ sau:

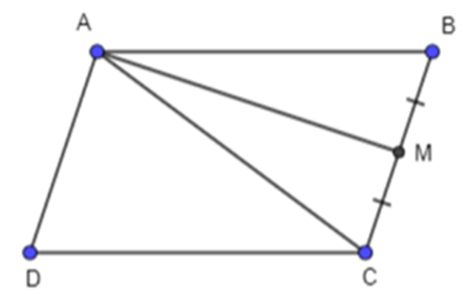
Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị vecto AM theo vecto AB (ảnh 1)

Gọi E là điểm đối xứng với A qua M. Khi đó ABEC là hình bình hành

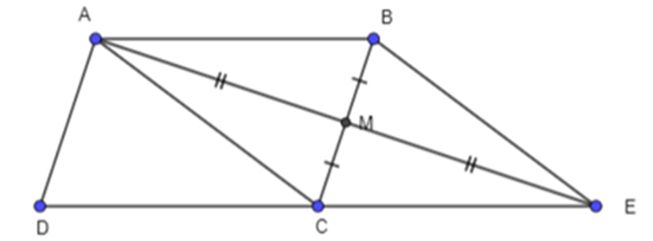
Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị vecto AM theo vecto AB (ảnh 2)

Ta có: \[\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AC}}} {\rm{ = }}\overrightarrow {{\rm{AE}}} \] (quy tắc hình bình hành)

Mà \[\overrightarrow {{\rm{AE}}} {\rm{ = 2}}\overrightarrow {{\rm{AM}}} \]

\[ \Rightarrow \overrightarrow {{\rm{AM}}} {\rm{ = }}\frac{{\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AC}}} }}{{\rm{2}}}\]

Ta lại có: \[\overrightarrow {{\rm{AC}}} {\rm{ = }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AD}}} \] (quy tắc hình bình hành)

\[ \Rightarrow \overrightarrow {{\rm{AM}}} {\rm{ = }}\frac{{\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AD}}} }}{{\rm{2}}}{\rm{ = }}\frac{{{\rm{2}}\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AD}}} }}{{\rm{2}}}{\rm{ = }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\frac{{\rm{1}}}{{\rm{2}}}\overrightarrow {{\rm{AD}}} {\rm{.}}\]

Vậy \[\overrightarrow {{\rm{AM}}} {\rm{ = }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\frac{{\rm{1}}}{{\rm{2}}}\overrightarrow {{\rm{AD}}} {\rm{.}}\]

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Số 0 và số 1 có phải số chính phương không?

Xem đáp án

Lời giải

O là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 0 = 0

1 là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 1 = 1

Câu 2

Hai góc tương ứng là gì?

Xem đáp án

Lời giải

Hai góc tương ứng là hai góc của hai tam giác khác nhau.

Hai góc đó bằng nhau và nằm trong hai tam giác bằng nhau.

Câu 3

Cho tam giác MNP, gọi K là điểm thuộc đoạn thẳng NP sao cho \[{\rm{NK = }}\frac{1}{4}{\rm{NP}}\]và I là trung điểm của đoạn thẳng MK. Mệnh đề nào dưới đây đúng?

A. \[{\rm{3}}\overrightarrow {{\rm{IM}}} {\rm{ + 4}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]

B. \[\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + 4}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]

C. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]

D. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + }}\overrightarrow {{\rm{IN}}} {\rm{ + 3}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]

Lời giải