Cho \[\Delta ABC\]vuông tại A. Gọi M là trung điểm của BC. Từ M hạ MP vuông góc với AB, \[{\rm{P }} \in {\rm{ AB}}\], \(MQ \bot AC\left( {Q \in AC} \right)\) R đối xứng M qua P
a, AQMP là hình gì ? Vì sao?
b, AMBR là hình gì ? Vì sao?
c, Điều kiện để tâm giác ANG để AQM P là hình vuông
Cho \[\Delta ABC\]vuông tại A. Gọi M là trung điểm của BC. Từ M hạ MP vuông góc với AB, \[{\rm{P }} \in {\rm{ AB}}\], \(MQ \bot AC\left( {Q \in AC} \right)\) R đối xứng M qua P
a, AQMP là hình gì ? Vì sao?
b, AMBR là hình gì ? Vì sao?
c, Điều kiện để tâm giác ANG để AQM P là hình vuông
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
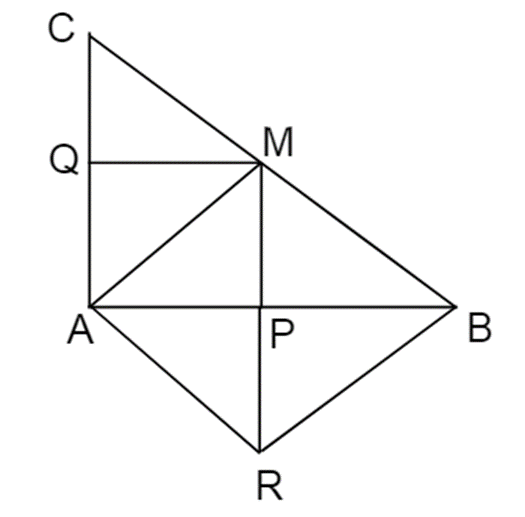
a) Ta có: \(\Delta ABC\)vuông tại A
\( \Rightarrow \widehat {\rm{A}}{\rm{ = 9}}{{\rm{0}}^{\rm{o}}}\)
MP vuông góc AB \( \Rightarrow \widehat {\rm{P}}{\rm{ = 9}}{{\rm{0}}^{\rm{o}}}\)
MQ vuông góc AC \[ \Rightarrow \widehat {\rm{Q}}{\rm{ = 9}}{{\rm{0}}^{\rm{o}}}\]
Ta có: \[\widehat {\rm{A}}{\rm{ = }}\widehat {\rm{P}}{\rm{ = }}\widehat {\rm{Q}}{\rm{ = 9}}{{\rm{0}}^{\rm{o}}}\]
Vậy AQMP là hình chữ nhật
b) Ta có: \(\Delta ABC\)vuông; AM là trung tuyến \[ \Rightarrow {\rm{AM = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{BC = MB}}\]
Vậy \(\Delta AMB\)cân mà MP là đường cao
→ MP cũng là trung tuyến
→ AP = BP.
Ta có: AP = BP; MP = PR (R đối xứng với M qua P); \[MP \bot AB\](hay\[MR \bot AB\])
→ AMBR là hình thoi
c) Để AQMP là hình vuông thì:
\[\widehat {{\rm{BAM}}}{\rm{ = }}\widehat {{\rm{ MAC}}}\]
hay AM là phân giác mà AM là trung tuyến
\( \Rightarrow \Delta ABC\)vuông cân tại A.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
O là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 0 = 0
1 là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 1 = 1
Lời giải
Hai góc tương ứng là hai góc của hai tam giác khác nhau.
Hai góc đó bằng nhau và nằm trong hai tam giác bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[{\rm{3}}\overrightarrow {{\rm{IM}}} {\rm{ + 4}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
B. \[\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + 4}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
C. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
D. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + }}\overrightarrow {{\rm{IN}}} {\rm{ + 3}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập