Câu hỏi:
12/07/2024 1,652
Cho \[\Delta ABC\]đều, đường cao AH. Lấy M nằm giữa B, C. Kẻ \[{\rm{MP }} \bot {\rm{ AB}}\]tại P ; \[{\rm{MQ }} \bot {\rm{AC}}\] tại Q. Gọi O là trung điểm AM. Chứng minh OHPQ là hình thoi. Tìm vị trí của M trên BC để PQ ngắn nhất.
Cho \[\Delta ABC\]đều, đường cao AH. Lấy M nằm giữa B, C. Kẻ \[{\rm{MP }} \bot {\rm{ AB}}\]tại P ; \[{\rm{MQ }} \bot {\rm{AC}}\] tại Q. Gọi O là trung điểm AM. Chứng minh OHPQ là hình thoi. Tìm vị trí của M trên BC để PQ ngắn nhất.
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
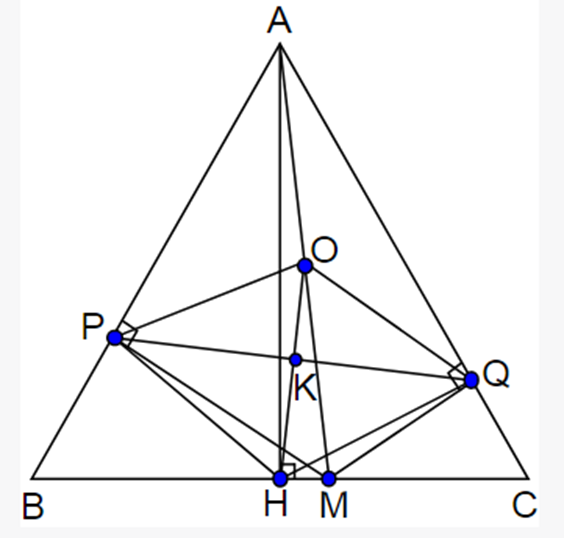
Xét \(\Delta APM\)vuông tại P ta có PO là đường trung tuyến ứng với cạnh huyền AM.
→ OA = OP = OM.
Tương tự cho \[\Delta AHM\]vuông tại H và \(\Delta AQM\)vuông tại Q ta có:
OA = OP = OH = OM = OQ (1)
→ \(\Delta AOP\)và \[\Delta AOH\]cân tại O.
Xét \(\Delta ABC\)đều ta có:
AH là đường cao cũng là đường phân giác
\[ \Rightarrow \widehat {{\rm{BAH}}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}\widehat {{\rm{BAC}}}{\rm{ = 3}}{{\rm{0}}^{\rm{0}}}\]
Ta có:
\[\widehat {{\rm{POM}}}{\rm{ = 2 }}\widehat {{\rm{PAO}}}\] ( góc ngoài của \(\Delta AOP\)cân tại O)
\[\widehat {{\rm{HOM}}}{\rm{\; = 2}}\widehat {{\rm{HAO}}}\] ( góc ngoài của \(\Delta AOH\)cân tại O)
\[ \Rightarrow {\rm{ }}\widehat {{\rm{POM}}}{\rm{ - }}\widehat {{\rm{HOM}}}{\rm{ = 2}}\left( {{\rm{ }}\widehat {{\rm{PAO}}}{\rm{ - }}\widehat {{\rm{HAO}}}} \right)\]
\[ \Rightarrow {\rm{ }}\widehat {{\rm{POH}}}{\rm{ = 2}}\widehat {{\rm{PAH}}}\]
Mà\[{\rm{ }}\widehat {{\rm{PAH}}}{\rm{ = 3}}{{\rm{0}}^{\rm{0}}}\]( cmt)
Nên \[\widehat {{\rm{POH}}}{\rm{ = 6}}{{\rm{0}}^{\rm{0}}}\]
Mặt khác OH = OP ( cmt)
\[ \Rightarrow {\rm{ \Delta POH}}\]đều.
→ PH = OP (2)
Tương tự ta có \[\Delta QOH\]đều
→ QH = OQ (3)
Từ (1), (2), (3) suy ra OP = OQ = PH = HQ
→ Tứ giác OPHQ là hình thoi ( tứ giác có 4 cạnh bằng nhau)
Gọi K là giao điểm của OH và PQ.
Do tứ giác OPHQ là hình thoi và K là giao điểm 2 đường chéo OH và PQ
Nên K là trung điểm của OH và PQ và \[{\rm{OH }} \bot {\rm{ PQ}}\]tại K.
\[ \Rightarrow {\rm{ OK = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{OH = }}\frac{{\rm{1}}}{{\rm{4}}}{\rm{AM}}\].
Xét \[\Delta OKP\]vuông tại K theo định lý Pitago thuận ta có:
\[{\rm{P}}{{\rm{K}}^{\rm{2}}}{\rm{\; = O}}{{\rm{P}}^{\rm{2}}}{\rm{\; - O}}{{\rm{K}}^{\rm{2}}}{\rm{\; = }}\frac{1}{4}{\rm{ A}}{{\rm{M}}^{\rm{2}}}{\rm{\; - }}\frac{1}{{16}}{\rm{ A}}{{\rm{M}}^{\rm{2}}}{\rm{\; = }}\frac{3}{{16}}{\rm{ A}}{{\rm{M}}^{\rm{2}}}\]
\( \Rightarrow {\rm{PK = }}\frac{{\sqrt {\rm{3}} }}{{\rm{4}}}{\rm{AM}}\)
\( \Rightarrow {\rm{PQ = }}\frac{{\sqrt {\rm{3}} }}{{\rm{2}}}{\rm{AM}}\)
→ PQ nhỏ nhất khi AM nhỏ nhất.
Mà AM nhỏ nhất khi AM = AH
→ M trùng với H thì PQ nhỏ nhất.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác MNP, gọi K là điểm thuộc đoạn thẳng NP sao cho \[{\rm{NK = }}\frac{1}{4}{\rm{NP}}\]và I là trung điểm của đoạn thẳng MK. Mệnh đề nào dưới đây đúng?
Xem đáp án »
27/02/2023
11,146
Câu 3:
Cho nửa đường tròn (O) đường kính AB = 2R. Vẽ đường thẳng d là tiếp tuyến của (O) tại B. Trên cung AB lấy điểm M tùy ý tia AM cắt d tại N. Gọi C là trung điểm của AM tia CO cắt d tại D.
a ) CMR OBNC nội tiếp.
b ) CMR NO vuông góc với AD.
c ) CMR CA . CN = CO . CD
d ) Xác định vị trí điểm M để (2AM + AN ) đạt GTNN.
Cho nửa đường tròn (O) đường kính AB = 2R. Vẽ đường thẳng d là tiếp tuyến của (O) tại B. Trên cung AB lấy điểm M tùy ý tia AM cắt d tại N. Gọi C là trung điểm của AM tia CO cắt d tại D.
a ) CMR OBNC nội tiếp.
b ) CMR NO vuông góc với AD.
c ) CMR CA . CN = CO . CD
d ) Xác định vị trí điểm M để (2AM + AN ) đạt GTNN.
Xem đáp án »
12/07/2024
6,467
Câu 7:
Cho hàm số y = x2 và y = mx + 4, với m là tham số.
a) Khi m = 3, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.
b) Chứng minh rằng với mọi giá trị m, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A1(x1,y1); A2 (x1 ,y2). Tìm tất cả các giá trị của m sao cho (y1)2 + (y2)2 = 72.
Cho hàm số y = x2 và y = mx + 4, với m là tham số.
a) Khi m = 3, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.
b) Chứng minh rằng với mọi giá trị m, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A1(x1,y1); A2 (x1 ,y2). Tìm tất cả các giá trị của m sao cho (y1)2 + (y2)2 = 72.
Xem đáp án »
12/07/2024
4,152
về câu hỏi!