Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau: \[y = \frac{1}{2}x\](d1) và \[{\rm{y = }}\frac{1}{2}{\rm{x + 3}}\](d2). Xác định b để đường thẳng (d3) y = 2x + b cắt (d2) tại điểm có tung độ và hoành độ đối nhau.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
+) Vẽ đồ thị hàm số \[\left( {{{\rm{d}}_{\rm{1}}}} \right){\rm{: y = - }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{x}}\]
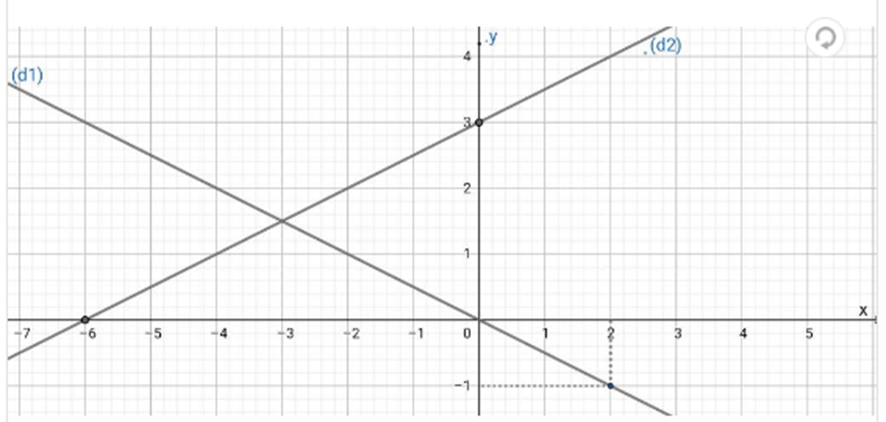
Với x = 0→ y = 0 ta có điểm (0; 0)
Với \[{\rm{x = 2}} \to {\rm{y = - }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{ }}{\rm{. 2 = - 1}}\] ta có điểm (2; −1)
Vẽ đường thẳng đi qua hai điểm (0; 0); (2; −1) ta được (d1)
+) Vẽ đồ thị hàm số\[\left( {{{\rm{d}}_{\rm{2}}}} \right){\rm{ : y = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{x + 3}}\]
Với x = 0 → y = 3 ta có điểm (0; 3)
Với \[{\rm{y = 0}} \Rightarrow \frac{{\rm{1}}}{{\rm{2}}}{\rm{x + 3 = 0}} \Rightarrow {\rm{x = - 6}}\] ta có điểm (−6; 0)
Vẽ đường thẳng đi qua hai điểm (0; 3); (−6; 0) ta được (d2)
+) Phương trình hoành độ giao điểm của \[\left( {{{\rm{d}}_{\rm{3}}}} \right){\rm{: y = 2x + b}}\]và \[\left( {{{\rm{d}}_{\rm{2}}}} \right){\rm{: y = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{x + 3}}\]là
\[{\rm{2x + b = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{x + 3}}\]
\[ \Leftrightarrow {\rm{2x - }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{x = 3 - b}}\]
\[ \Leftrightarrow \frac{{\rm{3}}}{{\rm{2}}}{\rm{x = 3 - b}}\]
\[ \Leftrightarrow {\rm{3x = 6 - 2b}}\]
\[ \Rightarrow {\rm{x = 2 - }}\frac{{\rm{2}}}{{\rm{3}}}{\rm{b}}\]
Thay \[{\rm{x = 2 - }}\frac{{\rm{2}}}{{\rm{3}}}{\rm{b}}\]vào \[\left( {{{\rm{d}}_{\rm{2}}}} \right){\rm{ : y = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{x + 3}}\]
\[ \Rightarrow {\rm{y = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{ }}{\rm{. }}\left( {{\rm{2 - }}\frac{{\rm{2}}}{{\rm{3}}}{\rm{b}}} \right){\rm{ + 3 = 1 - }}\frac{{\rm{1}}}{{\rm{3}}}{\rm{b + 3 = 4 - }}\frac{{\rm{1}}}{{\rm{3}}}{\rm{b}}\]
Vì giao điểm của (d2); (d3) có tung độ và hoành độ đối nhau
→ x + y = 0
\[ \Rightarrow {\rm{2 - }}\frac{{\rm{2}}}{{\rm{3}}}{\rm{b + 4 - }}\frac{{\rm{1}}}{{\rm{3}}}{\rm{b = 0}}\]
\[ \Leftrightarrow {\rm{ - }}\frac{{\rm{2}}}{{\rm{3}}}{\rm{b - }}\frac{{\rm{1}}}{{\rm{3}}}{\rm{b = - 4 - 2}}\]
\[ \Leftrightarrow - {\rm{b = - 6}}\]
\[ \Leftrightarrow {\rm{b = 6}}\]
Vậy \[{\rm{b = 6}}\]thỏa mãn đề bài
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
O là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 0 = 0
1 là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 1 = 1
Lời giải
Hai góc tương ứng là hai góc của hai tam giác khác nhau.
Hai góc đó bằng nhau và nằm trong hai tam giác bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[{\rm{3}}\overrightarrow {{\rm{IM}}} {\rm{ + 4}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
B. \[\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + 4}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
C. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
D. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + }}\overrightarrow {{\rm{IN}}} {\rm{ + 3}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập