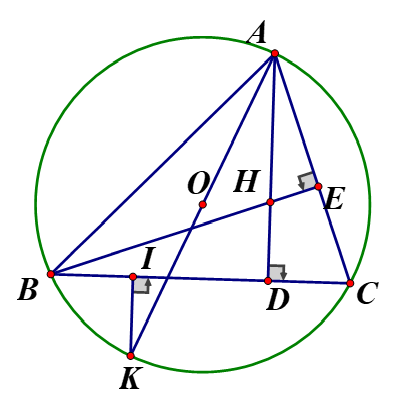
Cho có góc nhọn nội tiếp đường tròn .Hai đường cao AD và BE cắt nhau tại H
1 . Chứng minh : Tứ giác CEHD nội tiếp.
2 . Vẽ đường kính AH của đường tròn (O) .Chứng minh :
3 . Kẻ KI vuông góc với Chứng minh :
Cho có góc nhọn nội tiếp đường tròn .Hai đường cao AD và BE cắt nhau tại H
1 . Chứng minh : Tứ giác CEHD nội tiếp.
2 . Vẽ đường kính AH của đường tròn (O) .Chứng minh :
3 . Kẻ KI vuông góc với Chứng minh :
Quảng cáo
Trả lời:
là tứ giác nội tiếp
; (cùng chắn cung AB)
C/m (g-g)mà
Cộng (1) và
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
có nghiệm
Phương trình có nghiệm kép
Khi đó
Lời giải
Gọi x, y lần lượt là số ngày hai công nhân làm riêng xong công việc (x, y > 4).
Như vậy, trong 1 ngày người thứ nhất làm được (công việc), người thứ hai làm được (công việc).
Trong 1 ngày, cả hai người làm được (công việc)
Ta có phương trình: .
Nếu người thứ nhất làm một mình trong 7 ngày rồi nghỉ, người thứ hai làm tiếp phần việc còn lại trong một ngày nữa thì xong công việc, ta có phương trình: .
Ta có hệ phương trình:
(tm)
Vậy người thứ nhất làm một mình xong công việc trong 8 ngày, người thứ hai làm một mình xong công việc trong 8 ngày.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.