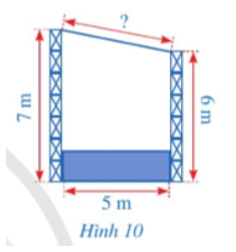
Quan sát Hình 1, bạn Đan khẳng định rằng: Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.
Bạn Đan đã dựa vào kiến thức nào để đưa ra khẳng định trên?
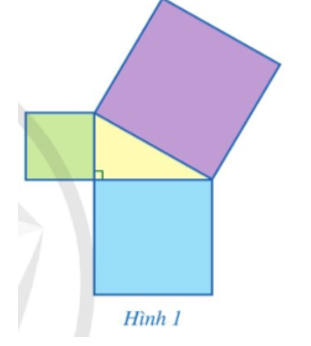
Quan sát Hình 1, bạn Đan khẳng định rằng: Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.
Bạn Đan đã dựa vào kiến thức nào để đưa ra khẳng định trên?

Quảng cáo
Trả lời:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Bạn Đan đã dựa vào Định lí Pythagore để đưa ra khẳng định “Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại”.
Thật vậy, giả sử A, B, C là ba đỉnh của tam giác (vuông tại A) và độ dài cạnh của các hình vuông lần lượt là a, b, c (hình vẽ).
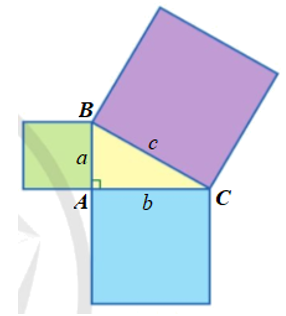
Diện tích hình vuông nhỏ màu xanh lá cây là: a2 (đơn vị diện tích).
Diện tích hình vuông nhỏ màu xanh nước biển là: b2 (đơn vị diện tích).
Diện tích hình vuông lớn màu tím là: c2 (đơn vị diện tích).
Do tam giác ABC vuông tại A nên theo định lí Pythagore ta có BC2 = AB2 + AC2
Hay c2 = a2 + b2.
Vậy diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Giả sử ABC là tam giác đều cạnh a (hình vẽ).
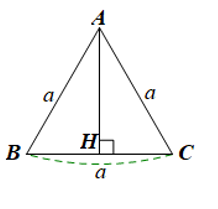
a) Vẽ đường cao AH của tam giác đều ABC.
Khi đó H là trung điểm của BC nên HB = HC = .
Xét tam giác AHC vuông tại H, theo định lí Pythagore ta có:
AC2 = AH2 + HC2
Suy ra AH2 = AC2 – HC2
Do đó .
Lời giải
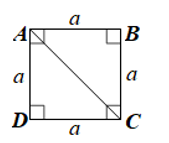
Do tam giác ABC vuông tại B nên theo định lí Pythagore ta có:
AC2 = AB2 + BC2 = a2 + a2 = 2a2
Suy ra .
Vậy độ dài đường chéo của hình vuông đó là .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.