Giải SBT Toán 8 Cánh Diều Tứ giác có đáp án

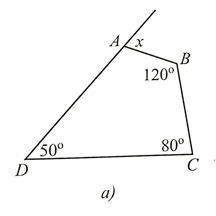
Trong tứ giác ABCD, ta có: \(\widehat {DAB} + \widehat B + \widehat C + \widehat D = 360^\circ \).

Do đó: \(\widehat {DAB} = 360^\circ - \left( {\widehat B + \widehat C + \widehat D} \right) = 360^\circ - \left( {120^\circ + 80^\circ + 50^\circ } \right) = 110^\circ \).

Ta có: \(\widehat {DAB} + x = 180^\circ \) (hai góc kề bù).

Suy ra \(x = 180^\circ - \widehat {DAB} = 180^\circ - 110^\circ = 70^\circ \).

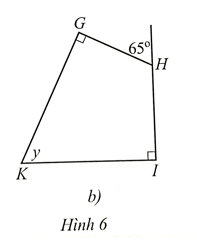
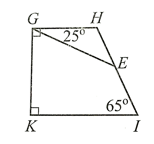
Ta có: \(\widehat {GHI} + 65^\circ = 180^\circ \) (hai góc kề bù).

Suy ra \(\widehat {GHI} = 180^\circ - 65^\circ = 115^\circ \).

Trong tứ giác GHIK, ta có: \(\widehat G + \widehat {GHI} + \widehat I + \widehat K = 360^\circ \).

Do đó: 90° + 115° + 90° + y = 360°

Hay y + 295° = 360°.

Suy ra y = 65°.

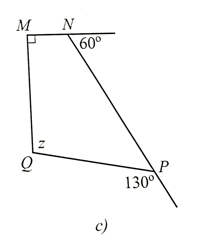
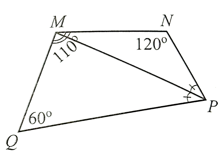
Ta có: \(\widehat {MNP} + 60^\circ = 180^\circ \) (hai góc kề bù). Suy ra \(\widehat {MNP} = 120^\circ \).

Ta cũng có: \(\widehat {NPQ} + 130^\circ = 180^\circ \) (hai góc kề bù). Suy ra \(\widehat {NPQ} = 50^\circ \).

Trong tứ giác MNPQ, ta có: \(\widehat M + \widehat {MNP} + \widehat {NPQ} + \widehat Q = 360^\circ \).

Do đó: 90° + 120° + 50° + z = 360°

Hay z + 260° = 360°.

Suy ra z = 100°.

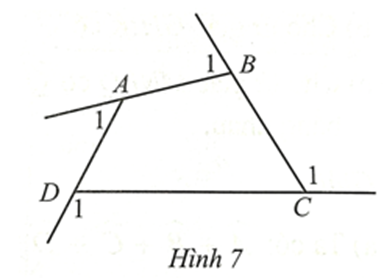
Trong tứ giác ABCD, ta có: \(\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {CDA} = 360^\circ \).

Ta có: \(\widehat {DAB} + \widehat {{A_1}} = \widehat {ABC} + \widehat {{B_1}} = \widehat {BCD} + \widehat {{C_1}} = \widehat {CDA} + \widehat {{D_1}} = 180^\circ \) (các cặp góc kề bù).

Suy ra:

\(\left( {180^\circ - \widehat {{A_1}}} \right) + \left( {180^\circ - \widehat {{B_1}}} \right) + \left( {180^\circ - \widehat {{C_1}}} \right) + \left( {180^\circ - \widehat {{D_1}}} \right) = 360^\circ \)

Hay \[720^\circ - \left( {\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}} \right) = 360^\circ \].

Do đó \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ \).

Vậy \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ \).

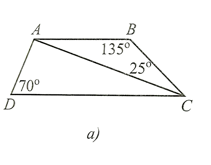
Trong tam giác ABC, ta có: \(\widehat {ABC} + \widehat {BAC} + \widehat {BCA} = 180^\circ \)

Suy ra \(\widehat {BAC} = 180^\circ - \left( {\widehat {ABC} + \widehat {BCA}} \right) = 180^\circ - \left( {135^\circ + 25^\circ } \right) = 20^\circ \).

Do AB // CD nên \(\widehat {ACD} = \widehat {BAC} = 20^\circ \) (hai góc so le trong).

Trong tam giác ACD, ta có: \(\widehat {ADC} + \widehat {ACD} + \widehat {DAC} = 180^\circ \)

Suy ra \(\widehat {DAC} = 180^\circ - \left( {\widehat {ADC} + \widehat {ACD}} \right) = 180^\circ - \left( {70^\circ - 20^\circ } \right) = 90^\circ \).

Vậy \(\widehat {DAC} = 90^\circ \).