Giải SBT Toán 8 Cánh Diều Hình thoi có đáp án
49 người thi tuần này 4.6 563 lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
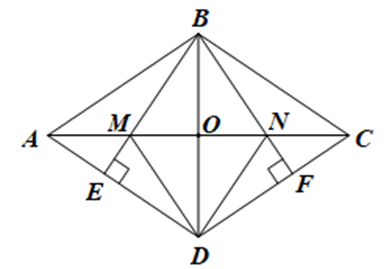
Gọi O là giao điểm của AC và BD.
Do ABCD là hình thoi nên AC vuông góc với BD tại trung điểm O của BD.
Suy ra AC là đường trung trực của BD. Do đó BM = DM, BN = DN.
Do ABCD là hình thoi nên BA = BC, \(\widehat {BAE} = \widehat {BCF}\).
Xét ∆ABE vuông tại E và ∆BCF vuông tại F có:
BA = BC, \(\widehat {BAE} = \widehat {BCF}\).
Do đó ∆ABE = ∆BCF (cạnh huyền – góc nhọn).
Suy ra \(\widehat {ABE} = \widehat {CBF}\) (hai góc tương ứng)
Mà \(\widehat {ABD} = \widehat {CBD}\) (do ABCD là hình thoi nên BD là đường phân giác của góc ABC) , suy ra \(\widehat {MBO} = \widehat {NBO}\).
Xét ∆MBO vuông tại O và ∆NBO vuông tại O có:
\(\widehat {MBO} = \widehat {NBO}\), cạnh BO chung
Do đó ∆MBO = ∆NBO (cạnh góc vuông – góc nhọn kề).
Suy ra BM = BN (hai cạnh tương ứng)
Mà BM = DM và BN = DN, suy ra BM = DM = BN = DN.
Tứ giác BMDN có BM = DM = BN = DN nên BMDN là hình thoi.
Lời giải
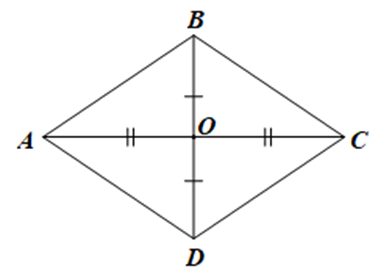
Xét hình thoi ABCD có \(AC = \frac{{18}}{5}{\rm{\;m}},BD = \frac{{27}}{{10}}{\rm{\;m}}\).
Gọi O là giao điểm của hai đường chéo AC và BD.
Do ABCD là hình thoi nên AC ⊥ BD, O là trung điểm của AC và BD.
Do O là trung điểm của AC nên \(OA = OC = \frac{{AC}}{2} = \frac{{\frac{{18}}{5}}}{2} = \frac{9}{5}{\rm{\;}}\)(m);
O là trung điểm của BD nên \(OB = OD = \frac{{BD}}{2} = \frac{{\frac{{27}}{{10}}}}{2} = \frac{{27}}{{20}}{\rm{\;}}\)(m).
Áp dụng định lý Pythagore cho tam giác OAB vuông tại O, ta có:
AB2 = OA2 + OB2.
Suy ra \(A{B^2} = {\left( {\frac{9}{5}} \right)^2} + {\left( {\frac{{27}}{{20}}} \right)^2} = \frac{{81}}{{25}} + \frac{{729}}{{400}} = \frac{{81}}{{16}}\)
Do đó \(AB = \sqrt {\frac{{81}}{{16}}} = \frac{9}{4}\,\,\left( {\rm{m}} \right)\).
Chu vi của hình thoi ABCD là: \(4AB = 4.\frac{9}{4} = 9\left( m \right)\).
Diện tích của hình thoi ABCD là: \(\frac{1}{2}AC.BD = \frac{1}{2}.\frac{{18}}{5}.\frac{{27}}{{10}} = \frac{{243}}{{50}}\left( {{{\rm{m}}^2}} \right)\).
Lời giải
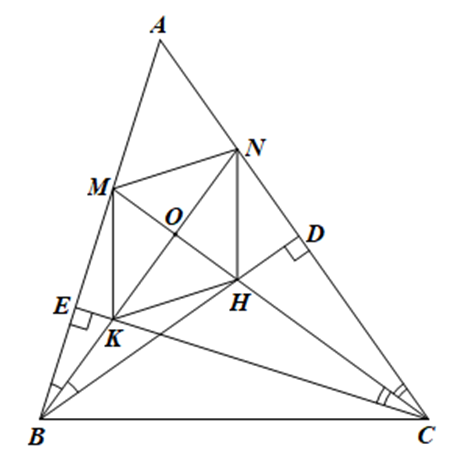
Do AD, CE là đường cao của ∆ABC nên AD ⊥ AC, CE ⊥ AB.
Do đó ∆ABD vuông tại D và ∆ACE vuông tại E nên \(\widehat {ABD} + \widehat A = \widehat {ACE} + \widehat A = 90^\circ \)
Suy ra \(\widehat {ABD} = \widehat {ACE}\).
Mà BN và CM lần lượt là tia phân giác của \(\widehat {ABD}\) và \(\widehat {ACE}\), suy ra \(\widehat {ABN} = \widehat {DBN} = \widehat {ACM} = \widehat {ECM}\).
Do ∆CEM vuông tại E nên \(\widehat {ECM} + \widehat {EMC} = 90^\circ \)
Suy ra \(\widehat {ABN} + \widehat {EMC} = 90^\circ \) hay \(\widehat {MBO} + \widehat {BMO} = 90^\circ \).
Trong tam giác MOB có: \(\widehat {MBO} + \widehat {BMO} + \widehat {BOM} = 180^\circ \)
Suy ra \(\widehat {BOM} = 180^\circ - \left( {\widehat {MBO} + \widehat {BMO}} \right) = 180^\circ - 90^\circ = 90^\circ \).
Vậy BN ⊥ CM.
Lời giải
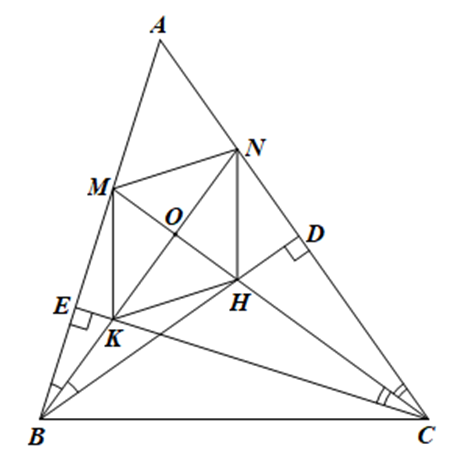
Xét ∆BMO vuông tại O và ∆BHO vuông tại O có:
Cạnh BO chung, \(\widehat {MBO} = \widehat {HBO}\)
Do đó ∆BMO = ∆BHO (cạnh góc vuông – góc nhọn kề).
Suy ra OM = OH (hai cạnh tương ứng)
Hay O là trung điểm của MH.
Tương tự ta chứng minh được ∆CNO = ∆CKO (cạnh góc vuông – góc nhọn kề).
Suy ra ON = OK (hai cạnh tương ứng)
Hay O là trung điểm của NK.
Tứ giác MNHK có hai đường chéo MH và NK cắt nhau tại trung điểm O của mỗi đường nên MNHK là hình bình hành.
Hình bình hành MNHK có MH ⊥ NK nên MNHK là hình thoi.
Lời giải
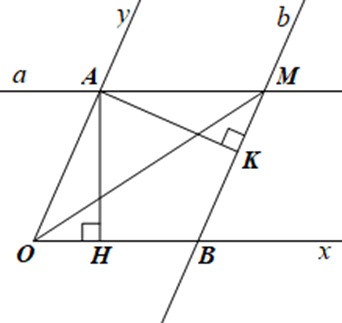
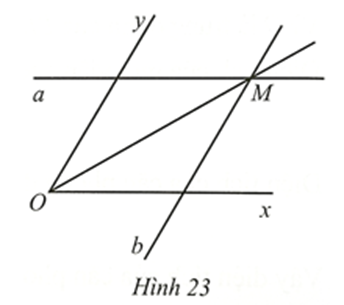
Gọi A là giao điểm của đường thẳng a với tia Oy, B là giao điểm của đường thẳng b với tia Ox.
Kẻ AH vuông góc với OB tại H, AK vuông góc với BM tại K.
Do khoảng cách giữa hai lề của thước là không đổi nên ta có AH = AK.
Do a // Ox nên AM // OB, b // Oy nên BM // OA
Tứ giác OAMB có AM // OB, BM // OA nên OAMB là hình bình hành.
Suy ra \(\widehat {AOB} = \widehat {AMB}\) hay \(\widehat {AOH} = \widehat {AMK}\).
Trong ∆AOH vuông tại H có: \(\widehat {OAH} + \widehat {AOH} = 90^\circ \);
Trong ∆AMK vuông tại K có: \(\widehat {MAK} + \widehat {AMK} = 90^\circ \).
Do đó \(\widehat {OAH} = \widehat {MAK}\).
Xét ∆AOH vuông tại H và ∆AMK vuông tại K có:
AH = AK, \(\widehat {OAH} = \widehat {MAK}\)
Do đó ∆AOH = ∆AMK (cạnh góc vuông – góc nhọn kề).
Suy ra OA = MA (hai cạnh tương ứng)
Hình bình hành OAMB có OA = MA nên OAMB là hình thoi.
Từ đó suy ra OM là tia phân giác của góc xOy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.