Giải SBT Toán 8 Cánh Diều Hình chữ nhật có đáp án
28 người thi tuần này 4.6 420 lượt thi 9 câu hỏi
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
6.5 K lượt thi
15 câu hỏi
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
2.8 K lượt thi
15 câu hỏi
10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)
1.2 K lượt thi
10 câu hỏi
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
3.4 K lượt thi
10 câu hỏi
10 Bài tập Tìm giá trị đơn thức khi biết giá trị của biến (có lời giải)
669 lượt thi
10 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
13.8 K lượt thi
18 câu hỏi
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
2.1 K lượt thi
15 câu hỏi
10 Bài tập Thu gọn đơn thức (có lời giải)
697 lượt thi
10 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
a) Sai. Vì hình thang có hai góc vuông có thể là hình chữ nhật hoặc hình thang vuông.
b) Đúng.
c) Đúng.
d) Sai. Vì tứ giác có 2 góc vuông chưa đủ điều kiện để khẳng định là hình chữ nhật.
Lời giải
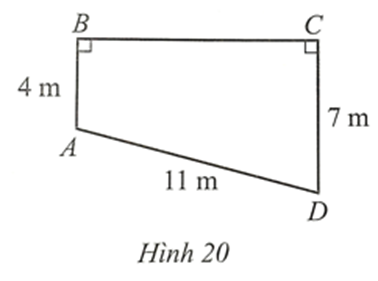
Kẻ AH vuông góc với CD tại H. Suy ra \(\widehat {AHC} = 90^\circ \).
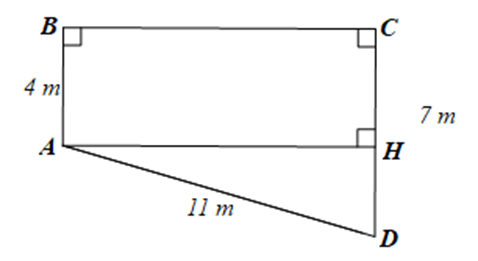
Ta có AB ⊥ BC, CD ⊥ BC nên \(\widehat {ABC} = \widehat {BCH} = 90^\circ \)
Tứ giác ABCH có \(\widehat {ABC} = \widehat {BCH} = \widehat {AHC} = 90^\circ \) nên ABCD là hình chữ nhật.
Suy ra CH = AB = 4 cm.
Ta có: CH + HD = CD
Do đó DH = CD ‒ CH = 7 ‒ 4 = 3 cm.
Áp dụng định lý Pythagore cho tam giác \(ADH\) vuông tại \(H\), ta có: AD2 = AH2 + DH2
Suy ra AH2 = AD2 ‒ DH2 = 112 ‒ 32 = 121 – 9 = 112
Do đó \(AH = \sqrt {112} {\rm{\;m}}\).
Mà BC = AH (vì ABCH là hình chữ nhật) nên \(BC = \sqrt {112} \approx 10,6\)(m).
Lời giải
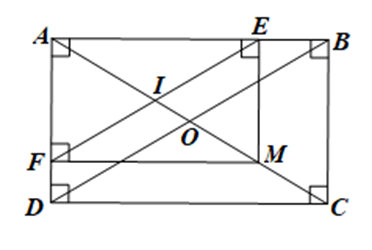
Gọi I là giao điểm của AM và EF.
Do ABCD là hình chữ nhật nên \(\widehat {DAB} = \widehat {ABC} = \widehat {BCD} = \widehat {ADC} = 90^\circ \)
Mà E, F lần lượt là hình chiếu của M lên AB, AD
Suy ra ME ⊥ AB, MF ⊥ AD. Do đó \(\widehat {AEM} = \widehat {MFA} = 90^\circ \)
Tứ giác AEMF có \(\widehat {FAE} = \widehat {AEM} = \widehat {MFA} = 90^\circ \) nên AEMF là hình chữ nhật.
Lời giải
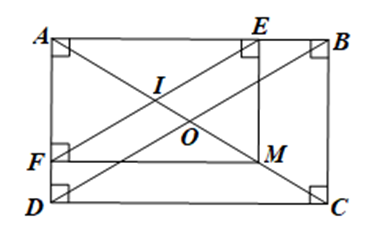
Gọi I là giao điểm của AM và EF.
Do ABCD và AEMF đều là hình chữ nhật nên OA = OB và IA = IE (2 đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường).
Suy ra tam giác OAB cân tại O và tam giác IAE cân tại I.
Do đó \(\widehat {OBA} = \widehat {OAB}\) và \(\widehat {IEA} = \widehat {IAE}\) hay \(\widehat {OBA} = \widehat {IEA}\).
Mà \(\widehat {OBA}\) và \(\widehat {IEA}\) nằm ở vị trí đồng vị, suy ra BD // EF.
Lời giải
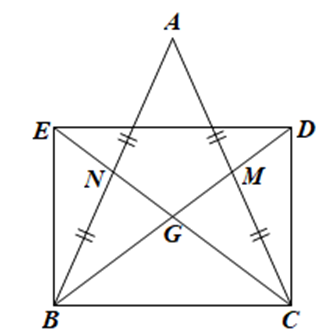
Do GD = GB, GE = GC nên G là trung điểm của BD và CE.
Tứ giác BEDC có hai đường chéo BD và CE cắt nhau tại trung điểm G của mỗi đường nên BEDC là hình bình hành.
BM, CN là các đường trung tuyến của ∆ABC nên M là trung điểm của AC, N là trung điểm của AB
Suy ra AM = CM, AN = BN
Lại có AB = AC (do ∆ABC cân tại A) nên BN = CM
Xét ∆BCM và ∆CBN có:
CM = BN (chứng minh trên), \[\widehat {ABC} = \widehat {ACB}\], cạnh BC chung
Do đó ∆BCM = ∆CBN (c.g.c). Suy ra BM = CN (hai cạnh tương ứng)
Do G là trọng tâm của tam giác ABC nên \(BG = \frac{2}{3}BM\) và \(CG = \frac{2}{3}CN\).
Do đó BG = CG.
Mà G là trung điểm của BD và CE, suy ra BD = CE.
Hình bình hành BEDC có BD = CE nên BEDC là hình chữ nhật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo