Giải SBT Toán 8 Cánh diều Bài 4. Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) có đáp án
61 người thi tuần này 4.6 544 lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Lời giải
Xét hàm số y = ax + b (a ≠ 0, b ≠ 0):
• Với x = 0 ta có y = b. Do đó đồ thị hàm số y = ax + b đi qua điểm P(0; b).
Với y = 0 ta có 0 = ax + b. Suy ra \(x = - \frac{b}{a}\).
Do đó đồ thị hàm số y = ax + b đi qua điểm \(Q\left( { - \frac{b}{a};0} \right)\).
Vì vậy phát biểu a là đúng và phát biểu b là sai.
• Với x = –1 ta có y = –a + b. Do đó đồ thị hàm số y = ax + b đi qua điểm M(‒1; ‒a + b).
Với x = –2 ta có y = –2a + b. Do đó đồ thị hàm số y = ax + b đi qua điểm K(‒2; ‒2a + b).
Vì vậy phát biểu c là đúng.
Vậy các phát biểu đúng là a, c.Lời giải
Lời giải
Gọi hệ số góc của các đường thẳng d1, d2, d3 lần lượt là a1, a2, a3.
Khi đó, ta có \({a_1} = 11,{a_2} = \sqrt 3 ,{a_3} = 2\).
Mà \(0 < \sqrt 3 < 2 < 11\), suy ra 0< a2 < a3 < a1.
Vậy các góc được sắp xếp theo thứ tự tăng dần là: α2; α3; α1.
Lời giải
Lời giải
a) Do đường thẳng d đi qua điểm A(1; 1) nên thay x = 1, y = 1 vào y = mx ‒ (2m + 2) ta có:
1 = m.1 ‒ (2m + 2)
Do đó 1 = m – 2m – 2
Suy ra m = –3.
Vậy với m = ‒3 thì đường thẳng d đi qua điểm A(1; 1).
b) Với m = ‒3, ta có đường thẳng d: y = ‒3x + 4.
Suy ra hệ số góc của đường thẳng d là a = –3 < 0. Vậy góc β là góc tù.
c) Để d và d’ cắt nhau thì m ≠ 3 ‒ 2m hay 3m ≠ 3
Suy ra m ≠ 1.
Vậy với \(m \ne 0,m \ne \frac{3}{2},m \ne 1\) thì d và d’ cắt nhau.
Lời giải
Lời giải
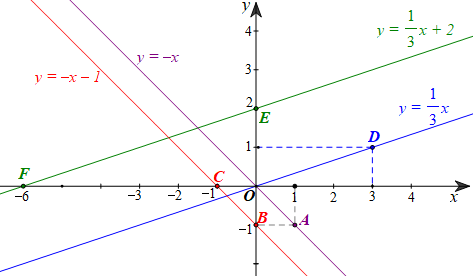
• Xét hàm số y = ‒x.
Với x = 1 thì y = ‒1, ta được điểm A(1; ‒1) thuộc đồ thị của hàm số y = ‒x.
Vậy đồ thị hàm số y = ‒x là đường thẳng đi qua hai điểm O(0; 0) và A(1; ‒1).
• Xét hàm số y = ‒x ‒ 1.
Với x = 0 thì y = ‒1, ta được điểm B(0; ‒1) thuộc đồ thị của hàm số y = ‒x ‒ 1.
Với y = 0 thì x = ‒1, ta được điểm C(‒1; 0) thuộc đồ thị của hàm số y = ‒x ‒ 1.
Vậy đồ thị hàm số y = ‒x ‒ 1 là đường thẳng đi qua hai điểm B(0; ‒1) và C(‒1; 0).
Tương tự ta có:
• Đồ thị hàm số \(y = \frac{1}{3}x\) là đường thẳng đi qua hai điểm O(0; 0) và D(3; 1);
• Đồ thị hàm số \(y = \frac{1}{3}x + 2\) là đường thẳng đi qua hai điểm E(0; 2) và F(‒6; 0).
Ta có các đồ thị trên như hình vẽ dưới đây:
Lời giải
Lời giải
Do đường thẳng y = ax + b (a ≠ 0) song song với đường thẳng y = 2x ‒ 5 nên a = 2 (thoả mãn) và b ≠ ‒5.
Mà đường thẳng y = ax + b đi qua điểm A(2; 0), suy ra 0 = 2.2 + b hay b = ‒4 (thoả mãn).
Do đó, đường thẳng cần tìm là y = 2x – 4.
Với x = 0 thì y = ‒4, ta được điểm B(0; ‒4) thuộc đồ thị của hàm số y = 2x ‒ 4.
Vậy đồ thị của hàm số y = 2x ‒ 4 là đường thẳng đi qua hai điểm A(2; 0) và B(0; ‒5).
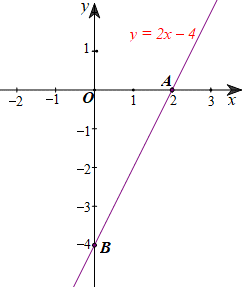
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.