Giải SBT Toán 8 Cánh diều Bài 2. Hình chóp tứ giác đều có đáp án
28 người thi tuần này 4.6 664 lượt thi 8 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
10.5 K lượt thi
10 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 8 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
3.5 K lượt thi
21 câu hỏi
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
16.1 K lượt thi
15 câu hỏi
Bộ 10 đề thi Cuối kì 1 Toán 8 Kết nối tri thức có đáp án - Đề 1
13.9 K lượt thi
18 câu hỏi
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
4 K lượt thi
10 câu hỏi
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
5.1 K lượt thi
10 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 8 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
2.8 K lượt thi
21 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 8 Cánh diều cấu trúc mới có đáp án - Đề 1
1.5 K lượt thi
21 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Lời giải
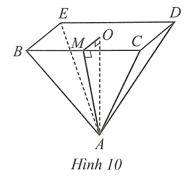
Do A.BCDE là hình chóp tứ giác đều có:
• mặt đáy BCDE là hình vuông;
• các mặt bên ABC, ACD, ADE, AEB là những tam giác cân tại A.
Khi đó trong mặt bên ABC có AM là trung đoạn nên AM ⊥ BC.
• AO là chiều cao nên DOAM vuông tại O, AM là cạnh huyền nên là cạnh lớn nhất
Do đó AO < AM.
Vậy phát biểu d là sai.
Lời giải
Lời giải
Diện tích xung quanh của hình chóp tứ giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn. Do đó phát biểu a là đúng, phát biểu b là sai.
Thể tích của hình chóp tứ giác đều bằng một phần ba tích của diện tích đáy với chiều cao.
Do đó phát biểu d là đúng, phát biểu c là sai.
Lời giải
Lời giải
Áp dụng công thức \({S_{xq}} = \frac{1}{2}.C\), trong đó Sxq là diện tích xung quanh, C là chu vi đáy, d là độ dài trung đoạn của hình chóp tứ giác đều, ta có: \(192 = \frac{1}{2}.C.8\).
Suy ra 4C = 192. Do đó C = 48 (cm).
Vậy độ dài cạnh đáy của hình chóp tứ giác đều đó là: 48 : 4 = 12 (cm).
Lời giải
Lời giải
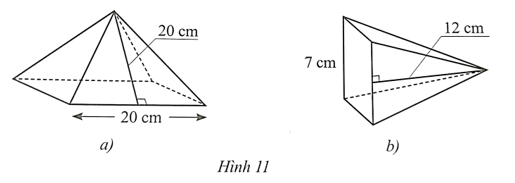
Diện tích xung quanh của hình chóp tứ giác đều ở Hình 11a là:
\(\frac{1}{2}.\left( {20.4} \right).20 = 800\)(cm2).
Diện tích xung quanh của hình chóp tứ giác đều ở Hình \(11b\) là:
\(\frac{1}{2}.\left( {7.4} \right).12 = 168\) (cm2).
Lời giải
Lời giải
Áp dụng công thức tính thể tích của chóp tứ giác đều \(V = \frac{1}{3}.S.h\), S là diện tích đáy, h là chiều cao của hình chóp tứ giác đều, V là thể tích.
Khi đó, thể tích của kim tự tháp Kheops khoảng:
\(\frac{1}{3}{.231^2}.146,5 = 2\,\,605\,\,795,5\) (m2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập