Câu hỏi:
13/07/2024 1,573
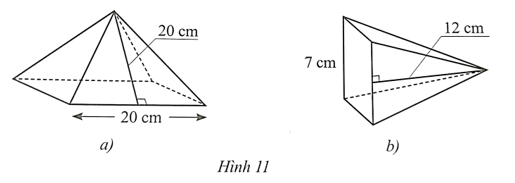
Cho hai hình chóp tứ giác đều S.ABCD và S.A'B'C'D' lần lượt có chiều cao SO và SO'. Biết AB = 2a, A'B' = 3a, SO = 2b, SO' =3b (Hình 12). Tính tỉ số thể tích của hình chóp tứ giác đều S.ABCD và S.A'B'C'D'. Biết rằng a và b cùng đơn vị đo.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Thể tích của hình chóp tứ giác đều S.ABCD là:
\(V = \frac{1}{3}.{S_{ABCD}}.SO = \frac{1}{3}.\left( {2a.2a} \right).2b = \frac{{8{a^2}b}}{3}{\rm{\;}}\) (đơn vị thể tích).
Thể tích của hình chóp tứ giác đều S.A’B’C’D’ là:
\(V' = \frac{1}{3}.{S_{A'B'C'D'}}.SO' = \frac{1}{3}.\left( {3a.3a} \right).3b = 9{a^2}b{\rm{\;}}\) (đơn vị thể tích).
Tỉ số thể tích của hình chóp tứ giác đều S.ABCD và S.A’B’C’D’ là:
\(\frac{V}{{V'}} = \frac{{8{a^2}b}}{3}:\left( {9{a^2}b} \right) = \frac{8}{{27}}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Áp dụng công thức \({S_{xq}} = \frac{1}{2}.C\), trong đó Sxq là diện tích xung quanh, C là chu vi đáy, d là độ dài trung đoạn của hình chóp tứ giác đều, ta có: \(192 = \frac{1}{2}.C.8\).
Suy ra 4C = 192. Do đó C = 48 (cm).
Vậy độ dài cạnh đáy của hình chóp tứ giác đều đó là: 48 : 4 = 12 (cm).
Lời giải
Lời giải
Đổi 1,4 m3 = 1 400 dm3
Áp dụng công thức \(V = \frac{1}{3}.S.h\), S là diện tích đấy, h là chiều cao của hình chóp tứ giác đều, V là thể tích.
Do đó ta có: \(1400 = \frac{1}{3}.S.42\)
Suy ra 14S = 1 400. Do đó S = 100 (dm).
Vậy độ dài cạnh đáy của hình chóp tứ giác đều đó là: \(\sqrt {100} = 10\)(dm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận