Câu hỏi:
13/07/2024 635
Cho tam giác ABC nhọn có các đường cao BD, CE. Tia phân giác của các góc ACE, ABD cắt nhau tại O và cắt AB, AC lần lượt tại M, N. Tia BN cắt CE tại K, tia CM cắt BD tại H. Chứng minh:
BN ⊥ CM;
Cho tam giác ABC nhọn có các đường cao BD, CE. Tia phân giác của các góc ACE, ABD cắt nhau tại O và cắt AB, AC lần lượt tại M, N. Tia BN cắt CE tại K, tia CM cắt BD tại H. Chứng minh:
BN ⊥ CM;
Câu hỏi trong đề: Giải SBT Toán 8 Cánh Diều Hình thoi có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
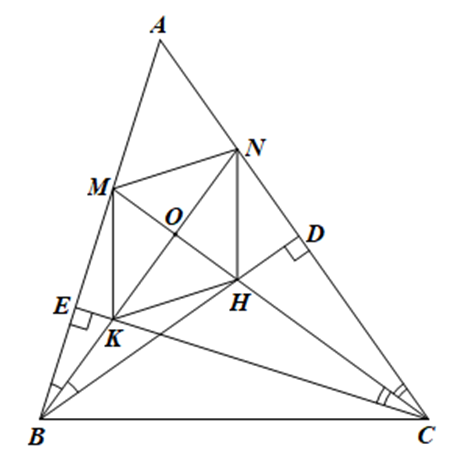
Do AD, CE là đường cao của ∆ABC nên AD ⊥ AC, CE ⊥ AB.
Do đó ∆ABD vuông tại D và ∆ACE vuông tại E nên \(\widehat {ABD} + \widehat A = \widehat {ACE} + \widehat A = 90^\circ \)
Suy ra \(\widehat {ABD} = \widehat {ACE}\).
Mà BN và CM lần lượt là tia phân giác của \(\widehat {ABD}\) và \(\widehat {ACE}\), suy ra \(\widehat {ABN} = \widehat {DBN} = \widehat {ACM} = \widehat {ECM}\).
Do ∆CEM vuông tại E nên \(\widehat {ECM} + \widehat {EMC} = 90^\circ \)
Suy ra \(\widehat {ABN} + \widehat {EMC} = 90^\circ \) hay \(\widehat {MBO} + \widehat {BMO} = 90^\circ \).
Trong tam giác MOB có: \(\widehat {MBO} + \widehat {BMO} + \widehat {BOM} = 180^\circ \)
Suy ra \(\widehat {BOM} = 180^\circ - \left( {\widehat {MBO} + \widehat {BMO}} \right) = 180^\circ - 90^\circ = 90^\circ \).
Vậy BN ⊥ CM.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
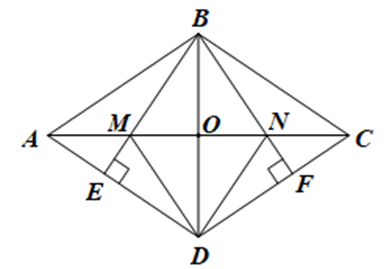
Gọi O là giao điểm của AC và BD.
Do ABCD là hình thoi nên AC vuông góc với BD tại trung điểm O của BD.
Suy ra AC là đường trung trực của BD. Do đó BM = DM, BN = DN.
Do ABCD là hình thoi nên BA = BC, \(\widehat {BAE} = \widehat {BCF}\).
Xét ∆ABE vuông tại E và ∆BCF vuông tại F có:
BA = BC, \(\widehat {BAE} = \widehat {BCF}\).
Do đó ∆ABE = ∆BCF (cạnh huyền – góc nhọn).
Suy ra \(\widehat {ABE} = \widehat {CBF}\) (hai góc tương ứng)
Mà \(\widehat {ABD} = \widehat {CBD}\) (do ABCD là hình thoi nên BD là đường phân giác của góc ABC) , suy ra \(\widehat {MBO} = \widehat {NBO}\).
Xét ∆MBO vuông tại O và ∆NBO vuông tại O có:
\(\widehat {MBO} = \widehat {NBO}\), cạnh BO chung
Do đó ∆MBO = ∆NBO (cạnh góc vuông – góc nhọn kề).
Suy ra BM = BN (hai cạnh tương ứng)
Mà BM = DM và BN = DN, suy ra BM = DM = BN = DN.
Tứ giác BMDN có BM = DM = BN = DN nên BMDN là hình thoi.
Lời giải
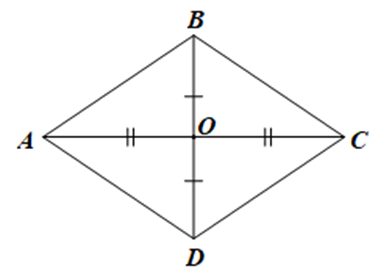
Xét hình thoi ABCD có \(AC = \frac{{18}}{5}{\rm{\;m}},BD = \frac{{27}}{{10}}{\rm{\;m}}\).
Gọi O là giao điểm của hai đường chéo AC và BD.
Do ABCD là hình thoi nên AC ⊥ BD, O là trung điểm của AC và BD.
Do O là trung điểm của AC nên \(OA = OC = \frac{{AC}}{2} = \frac{{\frac{{18}}{5}}}{2} = \frac{9}{5}{\rm{\;}}\)(m);
O là trung điểm của BD nên \(OB = OD = \frac{{BD}}{2} = \frac{{\frac{{27}}{{10}}}}{2} = \frac{{27}}{{20}}{\rm{\;}}\)(m).
Áp dụng định lý Pythagore cho tam giác OAB vuông tại O, ta có:
AB2 = OA2 + OB2.
Suy ra \(A{B^2} = {\left( {\frac{9}{5}} \right)^2} + {\left( {\frac{{27}}{{20}}} \right)^2} = \frac{{81}}{{25}} + \frac{{729}}{{400}} = \frac{{81}}{{16}}\)
Do đó \(AB = \sqrt {\frac{{81}}{{16}}} = \frac{9}{4}\,\,\left( {\rm{m}} \right)\).
Chu vi của hình thoi ABCD là: \(4AB = 4.\frac{9}{4} = 9\left( m \right)\).
Diện tích của hình thoi ABCD là: \(\frac{1}{2}AC.BD = \frac{1}{2}.\frac{{18}}{5}.\frac{{27}}{{10}} = \frac{{243}}{{50}}\left( {{{\rm{m}}^2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 2
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận