Câu hỏi:
12/07/2024 7,417
Xếp ngẫu nhiên 5 học sinh A, B, C, D, E ngồi vào 1 dãy 5 ghế thẳng hàng (mỗi bạn ngồi 1 ghế). Tính xác suất để 2 bạn A và B không ngồi cạnh nhau.
Xếp ngẫu nhiên 5 học sinh A, B, C, D, E ngồi vào 1 dãy 5 ghế thẳng hàng (mỗi bạn ngồi 1 ghế). Tính xác suất để 2 bạn A và B không ngồi cạnh nhau.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xếp 5 học sinh A, B, C, D, E vào 1 dãy 5 ghế thẳng hàng có 5! cách xếp ⇒ n(Ω) = 5! =120.
Gọi X là biến cố: “2 bạn A và B không ngồi cạnh nhau” ⇒ Biến cố đối \(\overline X \): “ 2 bạn A và B ngồi cạnh nhau”
Buộc 2 bạn A và B coi là 1 phần tử, có 2! Cách đổi chỗ 2 bạn A và B trong buộc này.
Bài toán trở thành xếp 4 bạn (AB), C, D, E vào dãy 4 ghế thẳng hàng ⇒ Có 4! cách xếp.
\( \Rightarrow n\left( {\overline X } \right) = 2!.4! = 48\)
\( \Rightarrow P\left( {\overline X } \right) = \frac{{n\left( {\overline X } \right)}}{{n\left( \Omega \right)}} = \frac{{48}}{{120}} = \frac{2}{5}\)
Vậy P(X) = 1 – \(P\left( {\overline X } \right) = 1 - \frac{2}{5} = \frac{3}{5}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
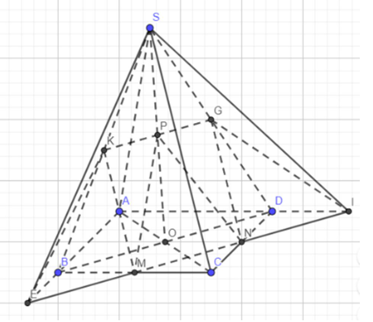
Gọi I, E lần lượt là giao điểm của MN với AD, AB
Qua P kẻ đường thẳng song song với BD cắt SB, SD lần lượt tại K, G
Ta có:
M, N lần lượt là trung điểm của BC, CD ⇒ MN là đường trung bình của ∆BCD ⇒ MN // BD
Mà KG // BD ⇒ MN // KG ⇒ K, G ∈ (MNP)
Ta có:
+) \(\left\{ {\begin{array}{*{20}{c}}{E = AB \cap MN \Rightarrow E \in \left( {SAB} \right) \cap \left( {MNP} \right)}\\{K \in SB;K \in \left( {MNP} \right) \Rightarrow K \in \left( {SAB} \right) \cap \left( {MNP} \right)}\end{array}} \right. \Rightarrow \left( {SAB} \right) \cap \left( {MNP} \right) = KE\)
+) \(\left\{ {\begin{array}{*{20}{c}}{I = AD \cap MN \Rightarrow I \in \left( {SAD} \right) \cap \left( {MNP} \right)}\\{G \in SD;G \in \left( {MNP} \right) \Rightarrow G \in \left( {SAD} \right) \cap \left( {MNP} \right)}\end{array}} \right. \Rightarrow \left( {SAD} \right) \cap \left( {MNP} \right) = IG\)
+) \(\left\{ {\begin{array}{*{20}{c}}{M,K \in \left( {MNP} \right)}\\{M,K \in \left( {SBC} \right)}\end{array}} \right. \Rightarrow \left( {SBC} \right) \cap \left( {MNP} \right) = MK\)
+) \(\left\{ {\begin{array}{*{20}{c}}{N,G \in \left( {MNP} \right)}\\{N,G \in \left( {SCD} \right)}\end{array}} \right. \Rightarrow \left( {SCD} \right) \cap \left( {MNP} \right) = NG\)
Vậy (SAB) ∩ (MNP) = KE; (SAD) ∩ (MNP) = IG; (SBC) ∩ (MNP) = MK; (SCD) ∩ (MNP) = NG.
Lời giải
\({\sin ^2}2^\circ + {\sin ^2}4^\circ + {\sin ^2}6^\circ + ... + {\sin ^2}84^\circ + {\sin ^2}86^\circ + {\sin ^2}88^\circ \)
\( = \left( {{{\sin }^2}2^\circ + {{\sin }^2}88^\circ } \right) + \left( {{{\sin }^2}4^\circ + {{\sin }^2}86^\circ } \right) + ... + \left( {{{\sin }^2}44^\circ + {{\sin }^2}46^\circ } \right)\)
\( = \left( {{{\sin }^2}2^\circ + {{\cos }^2}2^\circ } \right) + \left( {{{\sin }^2}4^\circ + {{\cos }^2}4^\circ } \right) + ... + \left( {{{\sin }^2}44^\circ + {{\cos }^2}44^\circ } \right)\) (do 2 góc phụ nhau sin góc này bằng cos góc kia)
= 1 + 1 + 1 +....+ 1 = 22 .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận