Cho tam giác ABC (AB > AC) có đường cao AH . Gọi M , N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh: MNPH là hình thang cân.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

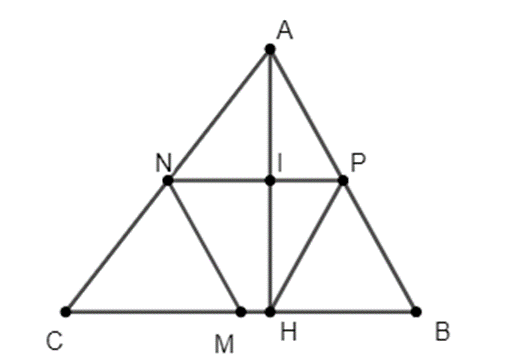
Cho tam giác ABC (AB > AC) có đường cao AH . Gọi M , N, P lần lượt là trung (ảnh 1)

Ta có:

N là trung điểm của AC;

P là trung điểm của AB.

Suy ra NP là đường trung bình của ∆ABC.

Suy ra MP // BC

Suy ra MNPH là hình thang (1).

Ta có:

\(\widehat B = \widehat {NMC}\) (đồng vị, AB // MN)

\(\widehat B = \widehat {PHB}\) (\(\Delta PHB\) cân)

Suy ra \(\widehat {NMC} = \widehat {PHB}\) \( \Rightarrow \widehat {NMH} = \widehat {PHM}\)(2)

Từ (1) và (2) suy ra được tứ giác MNPH là hình thang cân.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm x, biết: 3x(x – 1) + x – 1 = 0.

Xem đáp án

Lời giải

Ta có: 3x(x – 1) + x – 1 = 0

\( \Leftrightarrow \)3x(x – 1) + (x – 1) = 0

\( \Leftrightarrow \)(x – 1)(3x + 1) = 0

\( \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\3x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{{ - 1}}{3}\end{array} \right.\).

Câu 2

Tìm x, biết: 4x² – 25 – (2x – 5)(2x + 7) = 0.

Xem đáp án

Lời giải

4x² – 25 – (2x – 5)(2x + 7) = 0

\( \Leftrightarrow \)[(2x)² – 5²] – (2x – 5)(2x + 7) = 0

\( \Leftrightarrow \)(2x – 5)(2x + 5) – (2x – 5)(2x + 7) = 0

\( \Leftrightarrow \)(2x – 5)(2x + 5 – 2x – 7) = 0

\( \Leftrightarrow \)(2x – 5)(−2) = 0

\( \Leftrightarrow \)2x – 5 = 0

\( \Leftrightarrow x = \frac{5}{2}\).

Vậy \(x = \frac{5}{2}\).

Câu 3