Cho tam giác ABC. Chứng minh rằng:
a) \(\cot {\rm{A}} = \frac{{{b^2} + {c^2} - {a^2}}}{{4{\rm{S}}}}\).
b) \(\cot {\rm{A + cot B + cot C}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\).
Cho tam giác ABC. Chứng minh rằng:
a) \(\cot {\rm{A}} = \frac{{{b^2} + {c^2} - {a^2}}}{{4{\rm{S}}}}\).
b) \(\cot {\rm{A + cot B + cot C}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Áp dụng định lí côsin ta có: cos A = \(\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Ta có \(S = \frac{1}{2}bc\sin A\), suy ra \(\sin A = \frac{{2{\rm{S}}}}{{bc}}\)
Do đó cot A = \(\frac{{co{\rm{sA}}}}{{\sin {\rm{A}}}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}:\frac{{2{\rm{S}}}}{{bc}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}.\frac{{bc}}{{2{\rm{S}}}} = \frac{{{b^2} + {c^2} - {a^2}}}{{4{\rm{S}}}}\)
b) Chứng minh tương tự câu a ta có:
\(\cot B = \frac{{{a^2} + {c^2} - {b^2}}}{{4{\rm{S}}}}\); \(\cot C = \frac{{{a^2} + {b^2} - {c^2}}}{{4{\rm{S}}}}\)
Do đó:
\(\cot {\rm{A + cot B + cot C = }}\frac{{{c^2} + {b^2} - {a^2}}}{{4{\rm{S}}}} + \frac{{{a^2} + {c^2} - {b^2}}}{{4{\rm{S}}}} + \frac{{{a^2} + {b^2} - {c^2}}}{{4{\rm{S}}}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\)
Vậy \(\cot {\rm{A + cot B + cot C}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
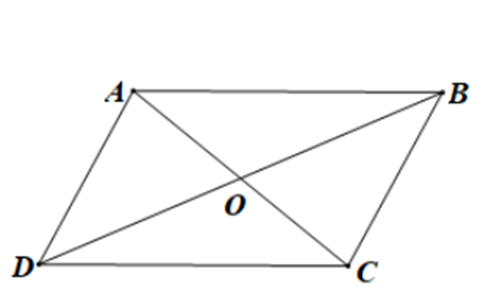
a) Vì ABCD là hình bình hành tâm O
Nên O là giao điểm của AC và BD, AB = CD, AD = BC
Suy ra O là trung điểm của AC và BD
Do đó OA = OC, OB = OD
Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {O{\rm{D}}} = (\overrightarrow {OA} + \overrightarrow {OC} ) + (\overrightarrow {OB} + \overrightarrow {O{\rm{D}}} ) = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)
b) Ta có \(\overrightarrow {OA} + \overrightarrow {BO} + \overrightarrow {CO} + \overrightarrow {{\rm{DO}}} = (\overrightarrow {OA} + \overrightarrow {CO} ) + (\overrightarrow {BO} + \overrightarrow {{\rm{DO}}} ) = \overrightarrow {CA} + \overrightarrow 0 = \overrightarrow {CA} \)
c) Vì ABCD là hình bình hành nên \(\overrightarrow {AB} + \overrightarrow {A{\rm{D}}} = \overrightarrow {AC} \)
Ta có
\(\overrightarrow {AC} + \overrightarrow {BD} + \overrightarrow {BA} + \overrightarrow {{\rm{DA}}} = (\overrightarrow {AC} + \overrightarrow {BA} + \overrightarrow {{\rm{DA}}} ) + \overrightarrow {B{\rm{D}}} = \left( {\overrightarrow {AB} + \overrightarrow {A{\rm{D}}} + \overrightarrow {BA} + \overrightarrow {DA} } \right) + \overrightarrow {B{\rm{D}}} \)
= \(\overrightarrow 0 + \overrightarrow {B{\rm{D}}} = \overrightarrow {B{\rm{D}}} \)
d) Ta có \(\overrightarrow {OA} + \overrightarrow {CB} + \overrightarrow {OC} + \overrightarrow {{\rm{AD}}} = (\overrightarrow {OA} + \overrightarrow {OC} ) + (\overrightarrow {CB} + \overrightarrow {{\rm{AD}}} ) = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)
Lời giải
Số gạo kho thứ nhất nhiều hơn số gạo kho thứ hai là:
17 – 8 = 9 (tấn)
Số gạo lúc đầu của kho thứ nhất là:
(155 + 9) : 2 = 82 (tấn)
Số gạo lúc đầu của kho thứ hai là
155 – 82 = 73 (tấn)
Vậy lúc đầu kho thứ nhất có 82 tấn gạo, kho thứ hai có 73 tấn gạo.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo