Cho ∆ABC cân tại B, AB = a, đường trung tuyến BM. Gọi I là trung điểm của BC, E là điểm đối xứng với M qua I.

a. Tứ giác MCEB là hình gì?

b. Chứng minh tứ giác ABEM là hình bình hành.

c. Tìm điều kiện của ∆ABC để tứ giác MCEB là hình vuông.

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

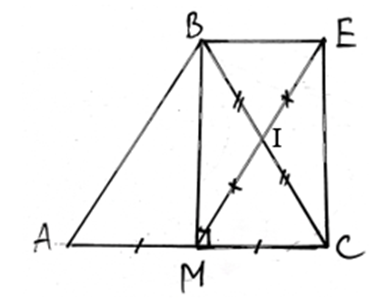
a. Xét tứ giác BMCE có 2 đường chéo

BC và ME cắt nhau tại trung điểm I của mỗi đường

⇒ Tứ giác BMCE là hình bình hành (1)

Vì ∆BAC cân tại B có M là trung điểm của AC ⇒ trung tuyến BM đồng thời là đồng thời là đường cao ⇒ \(\widehat {BMC} = 90^\circ \) (2)

Từ (1) và (2) ⇒ Tứ giác BMCE là hình chữ nhật.

b. Vì tứ giác BMCE là hình chữ nhật (cmt) ⇒ BE // MC

BE = MC; MC = MA ⇒ MA = BE

Có BE // MC ⇒ BE // AM (vì M ∈ AC)

Xét tứ giác ABEM có: \(\left\{ {\begin{array}{*{20}{c}}{BE//AM}\\{BE = AM}\end{array}} \right.\) ⇒ tứ giác ABEM là hình bình hành.

Vậy tứ giác ABEM là hình bình hành.

c. Tứ giác MCEB là hình vuông

Khi MB = MC ⇒ ∆BMC là tam giác vuông cân

\( \Rightarrow \widehat {MBC} = 45^\circ = \frac{{\widehat {ABC}}}{2} \Rightarrow \widehat {ABC} = 2\widehat {MBC} = 2.45^\circ = 90^\circ \)

⇒ ∆BAC là tam giác vuông cân

⇒ Tứ giác MCBE là hình vuông khi ∆BAC là tam giác vuông cân tại B.

Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xem đáp án

Lời giải

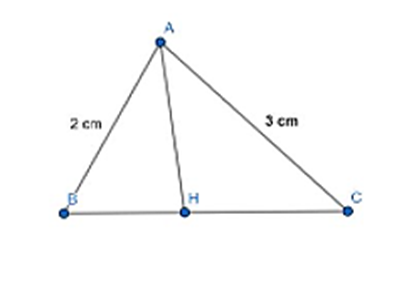
Cho tam giác ABC có AB = 2, AC = 3, góc A = 60 độ. Tính độ dài phân giác góc A (ảnh 1)

Áp dụng định lí hàm số côsin cho ∆ABC ta có: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.cos60^\circ = \sqrt 7 \)

Gọi AH là đường phân giác góc A.

Áp dụng tính chất đường phân giác cho ∆ABC: \(\frac{{AB}}{{AC}} = \frac{{BH}}{{HC}}\)

\(\frac{{AB}}{{BH}} = \frac{{AC}}{{HC}} = \frac{{AB + AC}}{{BH + HC}} = \frac{{2 + 3}}{{BC}} = \frac{5}{{\sqrt 7 }}\)

\( \Rightarrow BH = AB:\frac{5}{{\sqrt 7 }} = \frac{{2\sqrt 7 }}{5}\)

\(\cos \widehat B = \frac{{A{C^2} - A{B^2} - B{C^2}}}{{ - 2AB.BC}} = \frac{{\sqrt 7 }}{{14}}\)

Xét ∆ABH có: \(A{H^2} = A{B^2} + B{H^2} - 2.AB.BH.cos\widehat B = \frac{{108}}{{25}} \Rightarrow AH = \frac{{6\sqrt 3 }}{5}\).

Câu 2

Xem đáp án

Lời giải

\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\)

\(\frac{{\sin A}}{{\sin B}} = \frac{a}{b} = \frac{5}{4}\), b = 8

\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}}\)

\(\frac{{\sin A}}{{\sin C}} = \frac{a}{c} = \frac{5}{3}\), c = 6

Chu vi là: 8 + 6 + 10 = 24.

Câu 3