Cho 10 chữ số 0, 1, 2, 3,..., 9. Có bao nhiêu có tự nhiên lẻ gồm 6 chữ số khác nhau, nhỏ hơn 600000 được xây dựng từ 10 số trên.

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi số có 6 chữ số đó là \({a_1}{a_2}{a_3}{a_4}{a_5}{a_6}\)

TH1: \({a_6} \in \left\{ {1;3;5} \right\} \Rightarrow \)3 cách chọn

Mà \(1 \le {a_1} \le 5 \Rightarrow {a_1}\) có 4 cách chọn

Chọn 4 chữ số trong 8 chữ số gắn vào 4 vị trí còn lại là \(A_8^4\)

⇒ Số cách chọn trong TH1 là 3.4. \(A_8^4\)

TH2: \({a_6} \in \left\{ {7;9} \right\} \Rightarrow {a_6}\) có 2 cách chọn

\(1 \le {a_1} \le 5 \Rightarrow {a_1}\) có 5 cách chọn

Chọn 4 chữ số trong 8 chữ số gắn vào 4 vị trí còn lại là \(A_8^4\)

⇒ Số cách chọn trong Th2 là 2.5.\(A_8^4\).

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xem đáp án

Lời giải

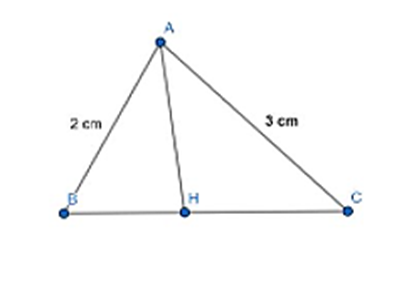
Cho tam giác ABC có AB = 2, AC = 3, góc A = 60 độ. Tính độ dài phân giác góc A (ảnh 1)

Áp dụng định lí hàm số côsin cho ∆ABC ta có: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.cos60^\circ = \sqrt 7 \)

Gọi AH là đường phân giác góc A.

Áp dụng tính chất đường phân giác cho ∆ABC: \(\frac{{AB}}{{AC}} = \frac{{BH}}{{HC}}\)

\(\frac{{AB}}{{BH}} = \frac{{AC}}{{HC}} = \frac{{AB + AC}}{{BH + HC}} = \frac{{2 + 3}}{{BC}} = \frac{5}{{\sqrt 7 }}\)

\( \Rightarrow BH = AB:\frac{5}{{\sqrt 7 }} = \frac{{2\sqrt 7 }}{5}\)

\(\cos \widehat B = \frac{{A{C^2} - A{B^2} - B{C^2}}}{{ - 2AB.BC}} = \frac{{\sqrt 7 }}{{14}}\)

Xét ∆ABH có: \(A{H^2} = A{B^2} + B{H^2} - 2.AB.BH.cos\widehat B = \frac{{108}}{{25}} \Rightarrow AH = \frac{{6\sqrt 3 }}{5}\).

Câu 2

Xem đáp án

Lời giải

\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\)

\(\frac{{\sin A}}{{\sin B}} = \frac{a}{b} = \frac{5}{4}\), b = 8

\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}}\)

\(\frac{{\sin A}}{{\sin C}} = \frac{a}{c} = \frac{5}{3}\), c = 6

Chu vi là: 8 + 6 + 10 = 24.

Câu 3