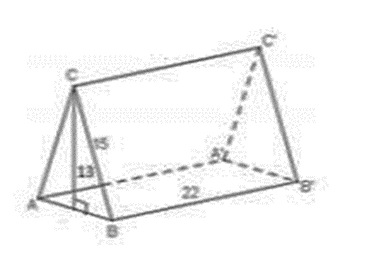
Một cục chặn giấy bằng sắt (hình vẽ) có dạng một lăng trụ đứng có chiều cao 22 cm, đáy là một tam giác cân (∆CAB) có chiều cao là 13 cm, cạnh bên dài 15 cm.

a. Tính độ dài cạnh AB (làm tròn đến phần trăm).

b. Tính diện tích phần sơn phủ cục chặn giấy (làm tròn đến\(c{m^3}\)).

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a. Độ dài \(AB = 2\sqrt {{{15}^2} - {{13}^2}} = 4\sqrt {14} \approx 14,97\)

b. Chu vi ∆CAB = 15 x 2 + \(4\sqrt {14} = 30 + 4\sqrt {14} \)

Diện tích xung quanh là: \(\left( {30 + 4\sqrt {14} } \right)x22 = 660 + 88\sqrt {14} \left( {c{m^2}} \right)\)

Diện tích 2 đáy là: \(13x\sqrt {14} :2 = 26\sqrt {14} \left( {c{m^2}} \right)\)

Diện tích sơn là: \(660 + 88\sqrt {14} + 26\sqrt {14} = 660 + 114\sqrt {14} \approx 1086,55\left( {c{m^2}} \right)\).

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xem đáp án

Lời giải

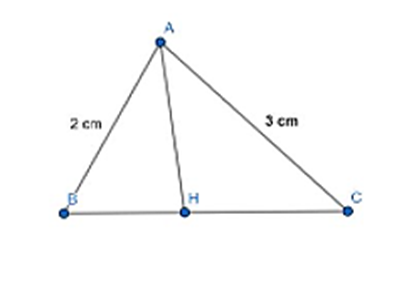
Cho tam giác ABC có AB = 2, AC = 3, góc A = 60 độ. Tính độ dài phân giác góc A (ảnh 1)

Áp dụng định lí hàm số côsin cho ∆ABC ta có: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.cos60^\circ = \sqrt 7 \)

Gọi AH là đường phân giác góc A.

Áp dụng tính chất đường phân giác cho ∆ABC: \(\frac{{AB}}{{AC}} = \frac{{BH}}{{HC}}\)

\(\frac{{AB}}{{BH}} = \frac{{AC}}{{HC}} = \frac{{AB + AC}}{{BH + HC}} = \frac{{2 + 3}}{{BC}} = \frac{5}{{\sqrt 7 }}\)

\( \Rightarrow BH = AB:\frac{5}{{\sqrt 7 }} = \frac{{2\sqrt 7 }}{5}\)

\(\cos \widehat B = \frac{{A{C^2} - A{B^2} - B{C^2}}}{{ - 2AB.BC}} = \frac{{\sqrt 7 }}{{14}}\)

Xét ∆ABH có: \(A{H^2} = A{B^2} + B{H^2} - 2.AB.BH.cos\widehat B = \frac{{108}}{{25}} \Rightarrow AH = \frac{{6\sqrt 3 }}{5}\).

Câu 2

Xem đáp án

Lời giải

\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\)

\(\frac{{\sin A}}{{\sin B}} = \frac{a}{b} = \frac{5}{4}\), b = 8

\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}}\)

\(\frac{{\sin A}}{{\sin C}} = \frac{a}{c} = \frac{5}{3}\), c = 6

Chu vi là: 8 + 6 + 10 = 24.

Câu 3