Giải phương trình nghiệm nguyên: \(2{x^2} + {y^2} - 2xy - 2x + y = 4\).

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

\(2{x^2} + {y^2} - 2xy - 2x + y = 4 \Leftrightarrow 2\left( {2{x^2} + {y^2} - 2xy - 2x + y} \right) = 2.4\)

\( \Leftrightarrow 4{x^2} + 2{y^2} - 4xy - 4x + 2y = 8 \Leftrightarrow \left( {4{x^2} + {y^2} + 1 - 4xy - 4x + 2y} \right) + {y^2} = 8 + 1\)

\( \Leftrightarrow {\left( {2x - y - 1} \right)^2} + {y^2} = 9\)

Vì x; y ∈ ℤ \( \Rightarrow {\left( {2x - y - 1} \right)^2};{y^2} \in Z \Rightarrow {\left( {2x - y - 1} \right)^2} + {y^2} = 9 = {\left( { - 3} \right)^2} + {0^2} = {3^2} + {0^2}\)

TH1: \(\left\{ {\begin{array}{*{20}{c}}{{{\left( {2x - y - 1} \right)}^2} = {{\left( { - 3} \right)}^2}}\\{{y^2} = {0^2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - 1\left( {TM} \right)}\\{y = 0\left( {TM} \right)}\end{array}} \right.\)

TH2:\(\left\{ {\begin{array}{*{20}{c}}{{{\left( {2x - y - 1} \right)}^2} = {3^2}}\\{{y^2} = {0^2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 2\left( {TM} \right)}\\{y = 0\left( {TM} \right)}\end{array}} \right.\)

TH3: \(\left\{ {\begin{array}{*{20}{c}}{{{\left( {2x - y - 1} \right)}^2} = {0^2}}\\{{y^2} = {{\left( { - 3} \right)}^2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - 1\left( {TM} \right)}\\{y = - 3\left( {TM} \right)}\end{array}} \right.\)

TH4: \(\left\{ {\begin{array}{*{20}{c}}{{{\left( {2x - y - 1} \right)}^2} = {0^2}}\\{{y^2} = {3^2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 2\left( {TM} \right)}\\{y = 3\left( {TM} \right)}\end{array}} \right.\)

Vậy \(\left( {x;y} \right) = \left\{ {\left( { - 1;0} \right);\left( {2;0} \right);\left( { - 1; - 3} \right);\left( {2;3} \right)} \right\}\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho ∆ABC có AB = 2, AC = 3, \(\widehat A = 60^\circ \). Tính độ dài phân giác \(\widehat A\).

Xem đáp án

Lời giải

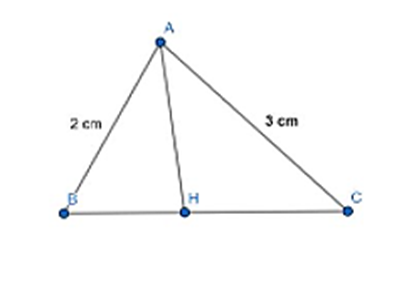
Cho tam giác ABC có AB = 2, AC = 3, góc A = 60 độ. Tính độ dài phân giác góc A (ảnh 1)

Áp dụng định lí hàm số côsin cho ∆ABC ta có: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.cos60^\circ = \sqrt 7 \)

Gọi AH là đường phân giác góc A.

Áp dụng tính chất đường phân giác cho ∆ABC: \(\frac{{AB}}{{AC}} = \frac{{BH}}{{HC}}\)

\(\frac{{AB}}{{BH}} = \frac{{AC}}{{HC}} = \frac{{AB + AC}}{{BH + HC}} = \frac{{2 + 3}}{{BC}} = \frac{5}{{\sqrt 7 }}\)

\( \Rightarrow BH = AB:\frac{5}{{\sqrt 7 }} = \frac{{2\sqrt 7 }}{5}\)

\(\cos \widehat B = \frac{{A{C^2} - A{B^2} - B{C^2}}}{{ - 2AB.BC}} = \frac{{\sqrt 7 }}{{14}}\)

Xét ∆ABH có: \(A{H^2} = A{B^2} + B{H^2} - 2.AB.BH.cos\widehat B = \frac{{108}}{{25}} \Rightarrow AH = \frac{{6\sqrt 3 }}{5}\).

Câu 2

Cho \(\cos x = \frac{2}{{\sqrt 5 }},0 < x < \frac{\pi }{2}\). Tính các giá trị lượng giác của góc x.

Xem đáp án

Lời giải

Ta có: 0 < x < \(\frac{\pi }{2} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\sin x > 0}\\{\cos x > 0}\end{array}} \right.\)

+) \({\cos ^2}x + {\sin ^2}x = 1 \Leftrightarrow {\frac{2}{{\sqrt 5 }}^2} + {\sin ^2}x = 1\)

\( \Leftrightarrow {\sin ^2}x = \frac{1}{5} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin x = \frac{1}{{\sqrt 5 }}\left( {TM} \right)}\\{\sin x = - \frac{1}{{\sqrt 5 }}\left( L \right)}\end{array}} \right.\)

\( + )1 + {\cos ^2}x = \frac{1}{{{{\cos }^2}x}} \Leftrightarrow 1 + {\cos ^2}x = \frac{1}{{{{\left( {\frac{2}{{\sqrt 5 }}} \right)}^2}}}\)

\( \Leftrightarrow {\tan ^2}x = \frac{1}{4} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\tan x = \frac{1}{2}(TM)}\\{{\mathop{\rm t}\nolimits} = - \frac{1}{2}(L)}\end{array}} \right.\).

Câu 3