Câu hỏi:
12/07/2024 3,333
Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B.
a) Chứng minh tứ giác ABHM nội tiếp.
b) Chứng minh OA.OB = OH.OM = R2.
c) Chứng minh tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.
Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B.
a) Chứng minh tứ giác ABHM nội tiếp.
b) Chứng minh OA.OB = OH.OM = R2.
c) Chứng minh tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
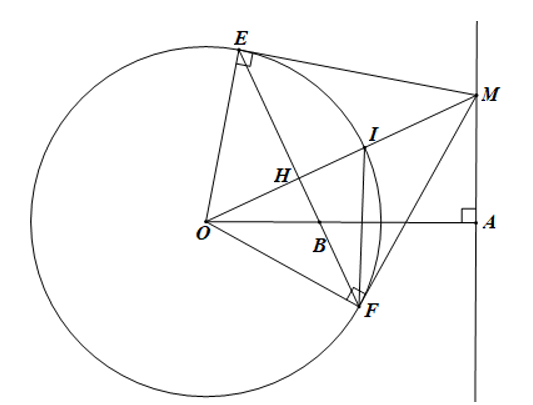
a) Do ME, MF là tiếp tuyến với đường tròn suy ra ME = MF nên M thuộc đường trung trực của EF.
Ta có OE = OF nên O thuộc đường trung trực của EF.
Do đó OM là đường trung trực của EF.
Þ EF ⊥ OM.
Tứ giác ABHM có , mà hai góc này ở vị trí đối nhau nên tứ giác này nội tiếp đường tròn bán kính MB.
b) Xét DOHB và DOAM có:
chung
(tỉ số đồng dạng)
Þ OA.OB = OH.OM (1)
Xét DOHE và DOEM có:
; chung
(tỉ số đồng dạng)
Þ OH.OM = OE2 (2)
Từ (1) và (2) suy ra OA.OB = OH.OM = OE2 = R2.
c) Gọi I là giao điểm của OM với đường tròn (O). Nối FI.
Ta có: (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung FI)
Do EF ⊥ OM nên suy ra (hai góc nội tiếp chắn hai cung bằng nhau)
Suy ra FI là phân giác của .
Lại có MI là phân giác của góc (do ME, MF là tiếp tuyến của (O)).
Do đó I là giao điểm của hai đường phân giác trong của tam giác MEF.
Þ I là tâm đường tròn nội tiếp tam giác MEF.
Mà I thuộc đường tròn (O) cố định. Suy ra đpcm.
d) Diện tích tam giác HBO là:
Xét DOHB và DOAM có:
là góc chung
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Một người đứng trên tháp quan sát của ngọn hải đăng cao 50 m nhìn về hướng Tây Nam, người đó quan sát hai lần một con thuyền đang hướng về ngọn hải đăng. Lần thứ nhất người đó nhìn thấy thuyền với góc hạ là 20°, lần thứ 2 người đó nhìn thấy thuyền với góc hạ là 30°. Hỏi con thuyền đã đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn đến chữ số thập phân thứ nhất)
Một người đứng trên tháp quan sát của ngọn hải đăng cao 50 m nhìn về hướng Tây Nam, người đó quan sát hai lần một con thuyền đang hướng về ngọn hải đăng. Lần thứ nhất người đó nhìn thấy thuyền với góc hạ là 20°, lần thứ 2 người đó nhìn thấy thuyền với góc hạ là 30°. Hỏi con thuyền đã đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn đến chữ số thập phân thứ nhất)
Xem đáp án »
12/07/2024
12,280
Câu 3:
Một mảnh đất hình chữ nhật bị xén đi một góc (hình vẽ), phần còn lại có dạng hình tứ giác ABCD với độ dài các cạnh là AB = 15m, BC = 19m, CD = 10m, DA = 20m. Diện tích mảnh đất ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị).
Một mảnh đất hình chữ nhật bị xén đi một góc (hình vẽ), phần còn lại có dạng hình tứ giác ABCD với độ dài các cạnh là AB = 15m, BC = 19m, CD = 10m, DA = 20m. Diện tích mảnh đất ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị).
Xem đáp án »
12/07/2024
10,927
Câu 4:
Cho (O), điểm A ở bên ngoài đường tròn. Vẽ các tiếp tuyến AB, AC và cát tuyến ADE. Gọi H là trung điểm của DE.
a) Chứng minh 5 điểm A, B, H, O, C cùng thuộc 1 đường tròn.
b) Chứng minh HA là tia phân giác của góc BHC.
c) Gọi I là giao của BC và DE. Chứng minh AB2 = AI.AH.
d) BH cắt (O) ở K. Chứng minh AE // CK.
Cho (O), điểm A ở bên ngoài đường tròn. Vẽ các tiếp tuyến AB, AC và cát tuyến ADE. Gọi H là trung điểm của DE.
a) Chứng minh 5 điểm A, B, H, O, C cùng thuộc 1 đường tròn.
b) Chứng minh HA là tia phân giác của góc BHC.
c) Gọi I là giao của BC và DE. Chứng minh AB2 = AI.AH.
d) BH cắt (O) ở K. Chứng minh AE // CK.
Xem đáp án »
12/07/2024
6,828
Câu 5:
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh hai tam giác ABM và ACM bằng nhau.
b) Chứng minh AM vuông góc với BC.
c) Chứng minh AM là phân giác của góc A.
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh hai tam giác ABM và ACM bằng nhau.
b) Chứng minh AM vuông góc với BC.
c) Chứng minh AM là phân giác của góc A.
Xem đáp án »
12/07/2024
5,275
Câu 6:
Cho đường tròn (O) dây cung BC (BC không là đường kính). Điểm A di động trên cung nhỏ BC (A khác B và C, độ dài cạnh AB khác AC). Kẻ đường kính AA' của đường tròn (O), D là chân đường vuông góc kẻ từ A đến BC. Hai điểm E, F lần lượt là chân đường vuông góc kẻ từ B, C đến AA'.
a) Chứng minh rằng 4 điểm A, B, D, E cùng nằm trên 1 đường tròn.
b) Chứng minh BD.AC = AD.A'C.
Cho đường tròn (O) dây cung BC (BC không là đường kính). Điểm A di động trên cung nhỏ BC (A khác B và C, độ dài cạnh AB khác AC). Kẻ đường kính AA' của đường tròn (O), D là chân đường vuông góc kẻ từ A đến BC. Hai điểm E, F lần lượt là chân đường vuông góc kẻ từ B, C đến AA'.
a) Chứng minh rằng 4 điểm A, B, D, E cùng nằm trên 1 đường tròn.
b) Chứng minh BD.AC = AD.A'C.
Xem đáp án »
12/07/2024
5,218
Câu 7:
Một lớp học có 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh. Xác suất của biến cố C: “Học sinh được chọn không giỏi Văn và Toán” là:
Một lớp học có 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh. Xác suất của biến cố C: “Học sinh được chọn không giỏi Văn và Toán” là:
Xem đáp án »
09/05/2023
4,227
về câu hỏi!