Cho \(a + \frac{5}{a} - 5 = b + \frac{6}{b} - 6\). (a khác 5, b khác 6). Chứng minh \(\frac{a}{b} = \frac{5}{6}\)

Lời giải

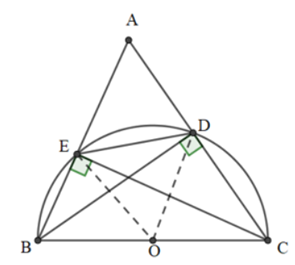
a) Gọi O là trung điểm của BC

\( \Rightarrow OB = OC = \frac{1}{2}BC\)  (1)

Xét tam giác DBC vuông tại D (do DB là đường cao của tam giác ABC)

Có DO là đường trung tuyến ứng với cạnh huyền BC

\( \Rightarrow OD = \frac{1}{2}BC\)  (2) (tính chất đường trung tuyến ứng với cạnh huyền)

Từ (1) và (2) suy ra \(OB = OC = OD = \frac{1}{2}BC\).

Do đó, ba điểm B, C, D cùng nằm trên đường tròn tâm O bán kính OB.

Xét tam giác BEC vuông tại E (do CE là đường cao của tam giác ABC)

Có EO là đường trung tuyến ứng với cạnh huyền BC

\(OE = \frac{1}{2}BC\) (3) (tính chất đường trung tuyến ứng với cạnh huyền)

Từ (1) và (3) suy ra \(OB = OC = OE = \frac{1}{2}BC\).

Do đó, ba điểm B, C, E cùng nằm trên đường tròn tâm O bán kính OB.

Do đó, bốn điểm B, C, E, D cùng nằm trên một đường tròn tâm O bán kính OB.

b) Xét đường tròn tâm O bán kính OB có đường kính BC.

Ta có DE là một dây cung không đi qua tâm O nên BC > DE do trong một đường tròn dây cung lớn nhất là đường kính.