Cho đường tròn tâm O, dây AB = 24 cm, dây AC = 20 cm (\[\widehat {BAC} < 90^\circ \] và điểm O nằm trong góc BAC). Gọi M là trung điểm AC. Khoảng cách từ M đến AB bằng 8 cm. Tính bán kính đường tròn.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải:
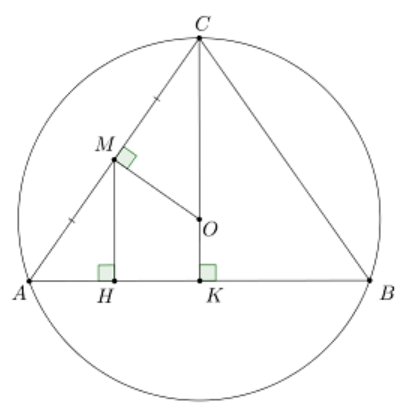
Kẻ MH ⊥ AB tại H.
Khi đó AM = 10 cm, MH = 8 cm.
Áp dụng định lý Py-ta-go vào tam giác AMH vuông tại H, ta có:
AM2 = MH2 + AH2
\[ \Rightarrow \] 102 = 82 + AH2
\[ \Rightarrow \] AH2 = 36
\[ \Rightarrow \] AH = 6 (cm)
Kẻ CK ⊥ AB tại K
Ta có: MH // CK (cùng vuông góc với AB), M là trung điểm AC, suy ra H là trung điểm AK
Do đó AK = 2AH = 12 cm = \[\frac{1}{2}\]AB.
Như vậy, CK vừa là đường cao, vừa là trung tuyến của tam giác ABC, cho nên ΔABC cân tại C.
Do đó, điểm O nằm trên CK.
Lại có MH là đường trung bình của tam giác ACK, suy ra CK = 2MH = 16 cm.
Xét ΔCMO và ΔCKA có:
\[\widehat C\] chung
\[\widehat {CMO} = \widehat {CKA} = 90^\circ \]
Suy ra: ΔCMO ᔕ ΔCKA (g.g).
\[ \Rightarrow \frac{{CM}}{{CK}} = \frac{{CO}}{{CA}} \Rightarrow \frac{{10}}{{16}} = \frac{R}{{20}}\]
Suy ra: R = 12,5 cm
Vậy R = 12,5 cm
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Đặt A = \(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{{16}} + \frac{1}{{32}} + \frac{1}{{64}} + \frac{1}{{128}} + \frac{1}{{256}}\)
\( \Rightarrow \) 2A = \(1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{{16}} + \frac{1}{{32}} + \frac{1}{{64}} + \frac{1}{{128}}\)
\( \Rightarrow \) 2A − A = 1 − \(\frac{1}{{256}}\)
\( \Rightarrow \) A = \(\frac{{255}}{{256}}\)
Lời giải
Lời giải:
Tổng của hai số gấp 5 lần bé nghĩa là số lớn gấp 4 lần số bé.
Ta có sơ đồ:
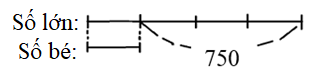
Theo sơ đồ, hiệu số phần bằng nhau là:
4 − 1 = 3 (phần)
Số lớn là : (705 : 3) × 4 = 940
Số bé là : 940 − 705 = 235
Đáp số: Số lớn: 940;
Số bé: 235.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.