Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải:
Xét n > 9 \( \Rightarrow \) A = 29 + 213 + 2n = 29(1 + 24 + 22n-9).
Thấy (1 + 24 + 22n-9) là số lẻ nên A chia hết cho 29 nhưng không chia cho 210 nên A không là số chính phương
• Xét n = 9, ta có:
A = 29 + 213 + 29 = 29(1 + 24 + 1) = 9. 210 = 962 là số chính phương.
• Xét n < 9, ta có:
A = 29 + 213 + 2n = 2n(29-n + 213-n + 1)
Do 29-n + 213-n + 1 là số lẻ và A là số chính phương nên 2n là số chính phương nên n là số chẵn, n ∈ ℕ* suy ra n ∈ {2; 4; 6; 8}
Khi đó A chính phương, 2n chính phương suy ra B = 29-n + 213-n + 1 là số chính phương Nhận xét số chính phương lẻ chỉ có thể tận cùng là 1; 5; 9.
• Với n = 2 \( \Rightarrow \) B = 27 + 211 + 1 = 2177 (loại)
• Với n = 4 \( \Rightarrow \) B = 25 + 29 + 1 = 545, thấy B chia hết cho 5 nhưng không chia hết cho 25 nên B không là số chính phương.
• Với n = 6 \( \Rightarrow \) B = 23 + 27 + 1 = 137 (loại)
• Với n = 8 \( \Rightarrow \) B =2 + 25 + 1 = 35 (loại)
Vậy n = 9
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Đặt A = \(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{{16}} + \frac{1}{{32}} + \frac{1}{{64}} + \frac{1}{{128}} + \frac{1}{{256}}\)
\( \Rightarrow \) 2A = \(1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{{16}} + \frac{1}{{32}} + \frac{1}{{64}} + \frac{1}{{128}}\)
\( \Rightarrow \) 2A − A = 1 − \(\frac{1}{{256}}\)
\( \Rightarrow \) A = \(\frac{{255}}{{256}}\)
Lời giải
Lời giải:
Tổng của hai số gấp 5 lần bé nghĩa là số lớn gấp 4 lần số bé.
Ta có sơ đồ:
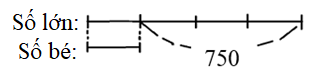
Theo sơ đồ, hiệu số phần bằng nhau là:
4 − 1 = 3 (phần)
Số lớn là : (705 : 3) × 4 = 940
Số bé là : 940 − 705 = 235
Đáp số: Số lớn: 940;
Số bé: 235.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.