Câu hỏi:
13/07/2024 1,612
Cho đường tròn tâm O đường kính AB, bán kính R. Từ điểm C trên tia đối của tia BA kẻ 1 cát tuyến cắt đường tròn ở E và D (E nằm giữa D và C) biết góc \(\widehat {DOE}\) = 90° và OC = 3R.
a) Tính độ dài CD, CE theo R.
b) Chứng minh CE.CD = CA.CB.
Cho đường tròn tâm O đường kính AB, bán kính R. Từ điểm C trên tia đối của tia BA kẻ 1 cát tuyến cắt đường tròn ở E và D (E nằm giữa D và C) biết góc \(\widehat {DOE}\) = 90° và OC = 3R.
a) Tính độ dài CD, CE theo R.
b) Chứng minh CE.CD = CA.CB.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
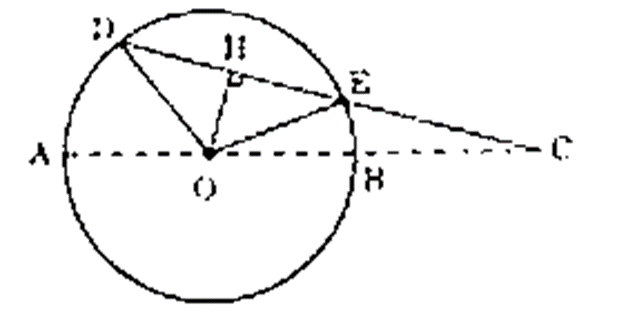
a) Tam giác DOE vuông tại O có OD = OE = R
Do đó: DE = \(\sqrt {O{D^2} + O{E^2}} \)= \(R\sqrt 2 \)
Xét tam giác EBC và tam giác DAC có:
\(\widehat C\)chung
\(\widehat {CEB} = \,\widehat {CAD} = \,\left( {180^\circ - \,\widehat {DEB}} \right)\)
⇒ \(\frac{{BC}}{{CD}} = \frac{{CE}}{{CA}}\, \Rightarrow \,CD = \frac{{AC\,.\,BC}}{{CE}}\)
\( \Rightarrow CD = \frac{{\left( {OA + OC} \right)\,.\,\left( {OC - OB} \right)}}{{DC - DE}} = \,\frac{{8{R^2}}}{{DC - R\sqrt 2 }}\)
Suy ra: DC2 – DC. \(R\sqrt 2 \)– 8R2 = 0
⇒ \(\left[ \begin{array}{l}CD = \frac{{R\left( {\sqrt {34} + \sqrt 2 } \right)}}{2}\\CD = \frac{{R\left( { - \sqrt {34} + \sqrt 2 } \right)}}{2}\end{array} \right.\)
Vì CD > 0 nên CD = \(\frac{{R\left( {\sqrt {34} + \sqrt 2 } \right)}}{2}\)
CE = DC – DE = \(\frac{{R\left( {\sqrt {34} + \sqrt 2 } \right)}}{2} - R\sqrt 2 \,\,\, = \,\,\,\frac{{R\left( {\sqrt {34} - \sqrt 2 } \right)}}{2}\)
b) Theo phần a ở trên ta có:
∆CEB ᔕ ∆CAD (g.g)
⇒ \(\frac{{BC}}{{CD}} = \frac{{CE}}{{CA}}\, \Rightarrow \,CD\,.\,CE = AC\,.\,BC\).
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm một số thập phân a biết rằng nếu chuyển dấu phẩy của nó sang bên trái 1 hàng ta được số b. Nếu chuyển dấu phẩy của nó sang bên phải một hàng ta được số c. Tổng của ba số a, b, c là 221,778.
Tìm một số thập phân a biết rằng nếu chuyển dấu phẩy của nó sang bên trái 1 hàng ta được số b. Nếu chuyển dấu phẩy của nó sang bên phải một hàng ta được số c. Tổng của ba số a, b, c là 221,778.
Xem đáp án »
13/07/2024
8,303
Câu 2:
Một đội xe chở hàng, hai xe đầu mỗi xe chở được 35 tạ hàng, ba xe sau mỗi xe chở được 45 tạ hàng. hỏi trung bình mỗi xe chở được bao nhiêu tạ hàng?
Một đội xe chở hàng, hai xe đầu mỗi xe chở được 35 tạ hàng, ba xe sau mỗi xe chở được 45 tạ hàng. hỏi trung bình mỗi xe chở được bao nhiêu tạ hàng?
Xem đáp án »
13/07/2024
7,492
Câu 3:
Cho abc ≠ 1 và \(\frac{{ab + 1}}{b}\,\, = \,\,\frac{{bc + 1}}{c}\,\, = \,\,\frac{{ca + 1}}{a}\). Chứng minh rằng a = b = c.
Cho abc ≠ 1 và \(\frac{{ab + 1}}{b}\,\, = \,\,\frac{{bc + 1}}{c}\,\, = \,\,\frac{{ca + 1}}{a}\). Chứng minh rằng a = b = c.
Xem đáp án »
13/07/2024
7,182
Câu 4:
Một ô tô đi trong \(\frac{1}{2}\) giờ được 21 km. Hỏi ô tô đó đi trong \(1\frac{1}{2}\) giờ được bao nhiêu ki–lô–mét?
Một ô tô đi trong \(\frac{1}{2}\) giờ được 21 km. Hỏi ô tô đó đi trong \(1\frac{1}{2}\) giờ được bao nhiêu ki–lô–mét?
Xem đáp án »
13/07/2024
6,007
Câu 5:
Tìm số lớn nhất có hai chữ số mà hiệu các chữ số của chúng bằng 6.
Tìm số lớn nhất có hai chữ số mà hiệu các chữ số của chúng bằng 6.
Xem đáp án »
13/07/2024
5,568
Câu 6:
Một mảnh đất hình chữ nhật có chiều dài 12,5 m, chiều rộng kém chiều dài 2,3 m. Tính chu vi và diện tích mảnh đất đó?
Một mảnh đất hình chữ nhật có chiều dài 12,5 m, chiều rộng kém chiều dài 2,3 m. Tính chu vi và diện tích mảnh đất đó?
Xem đáp án »
13/07/2024
5,541
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận