Câu hỏi:
12/07/2024 2,887Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
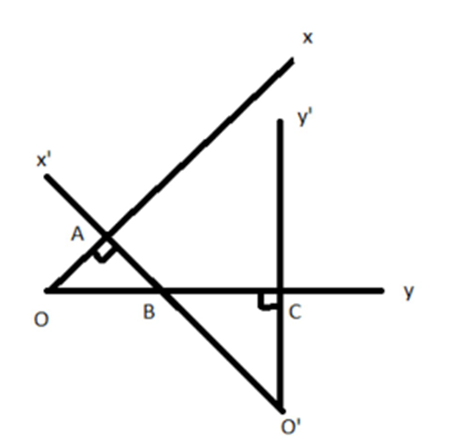
Ta có giả thiết 2 góc nhọn \[\widehat {xOy}\] và \[\widehat {x'O'y'}\] có các cặp cạnh tương ứng vuông góc: Ox ⊥ O’x’ và Oy ⊥ O’y’, cần chứng minh \[\widehat {xOy} = \widehat {x'O'y'}\].
Xét ΔOBA và ΔO’BC có
\[\widehat {OBA} = \widehat {O'BC}\] (đối đỉnh)
\[\widehat {OAB} = \widehat {O'CB} = 90^\circ \]
Do đó ΔOBA ᔕ ΔO’BC (g. g)
Suy ra \[\widehat {AOB} = \widehat {BO'C}\] hay \[\widehat {xOy} = \widehat {x'O'y'}\] (đpcm)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Xác suất để một viên trúng vòng 10 là: \[\sqrt[3]{{0,008}} \approx 0,0928\].
Xác suất để một viên trúng vòng 9 là:
1 − 0,4 − 0,0928 − 0,15 = 0,3572.
Các trường hợp xảy ra để thỏa mãn yêu cầu bài toán:
* Điểm ba lần bắn là 28 điểm, có 2 trường hợp: hai viên vòng 9 và một viên vòng 10 hoặc hai viên vòng 10 và một viên vòng 8.
Xác suất trong trường hợp này bằng:
\[\mathop P\nolimits_1 = C_3^2\,\,.\,\,{(0,3572)^2}\,.\,\,0,0928 + C_3^2\,\,.\,\,{(0,0928)^2}\,.\,\,0,15 \approx 0,0394\].
* Điểm ba lần bắn là 29 điểm, có 1 trường hợp: hai viên vòng 10 và một viên vòng 9. Xác suất trường hợp này bằng:
\[{P_2} = C_3^2\,\,.\,{(0,0928)^2}\,.\,\,0,3572 \approx 0,0092\].
* Điểm ba lần bắn là 30 điểm, có 1 trường hợp là cả ba viên vòng 10: Xác suất bằng 0,0008.
Vậy xác suất cần tìm bằng: P1 + P2 + 0,0008 = 0,00494.
Lời giải
Số gạo đó đủ cho số người ăn trong 1 ngày là:
50 . 10 = 500 (người)
Số gạo đã ăn đủ cho số người ăn trong 1 ngày là:
50 . 3 = 150 (người)
Số gạo còn lại đủ cho số người ăn trong 1 ngày là:
500 – 150 = 350 (người)
Sau ngày thứ 3 thì có số người ăn là:
50 + 20 = 70 (người)
Số ngày còn lại là:
10 – 3 = 7 (ngày)
Số suất ăn cần là:
70 . 7 = 490 (suất)
Cần thêm số suất ăn là:
490 – 350 = 140 (suất)
Đáp số: 140 suất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
Nhắn tin Zalo