Câu hỏi:
12/07/2024 5,945
Một đơn vị bộ đội chuẩn bị một số gạo đủ cho 50 người ăn trong 10 ngày, 3 ngày sau được tăng thêm 20 người. Hỏi đơn vị cần chuẩn bị bao nhiêu suất gạo nữa để cả đơn vị đủ ăn trong những ngày sau đó? (Số gạo mỗi người ăn trong một ngày là một suất gạo)
Một đơn vị bộ đội chuẩn bị một số gạo đủ cho 50 người ăn trong 10 ngày, 3 ngày sau được tăng thêm 20 người. Hỏi đơn vị cần chuẩn bị bao nhiêu suất gạo nữa để cả đơn vị đủ ăn trong những ngày sau đó? (Số gạo mỗi người ăn trong một ngày là một suất gạo)
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Số gạo đó đủ cho số người ăn trong 1 ngày là:
50 . 10 = 500 (người)
Số gạo đã ăn đủ cho số người ăn trong 1 ngày là:
50 . 3 = 150 (người)
Số gạo còn lại đủ cho số người ăn trong 1 ngày là:
500 – 150 = 350 (người)
Sau ngày thứ 3 thì có số người ăn là:
50 + 20 = 70 (người)
Số ngày còn lại là:
10 – 3 = 7 (ngày)
Số suất ăn cần là:
70 . 7 = 490 (suất)
Cần thêm số suất ăn là:
490 – 350 = 140 (suất)
Đáp số: 140 suất.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Xác suất để một viên trúng vòng 10 là: \[\sqrt[3]{{0,008}} \approx 0,0928\].
Xác suất để một viên trúng vòng 9 là:
1 − 0,4 − 0,0928 − 0,15 = 0,3572.
Các trường hợp xảy ra để thỏa mãn yêu cầu bài toán:
* Điểm ba lần bắn là 28 điểm, có 2 trường hợp: hai viên vòng 9 và một viên vòng 10 hoặc hai viên vòng 10 và một viên vòng 8.
Xác suất trong trường hợp này bằng:
\[\mathop P\nolimits_1 = C_3^2\,\,.\,\,{(0,3572)^2}\,.\,\,0,0928 + C_3^2\,\,.\,\,{(0,0928)^2}\,.\,\,0,15 \approx 0,0394\].
* Điểm ba lần bắn là 29 điểm, có 1 trường hợp: hai viên vòng 10 và một viên vòng 9. Xác suất trường hợp này bằng:
\[{P_2} = C_3^2\,\,.\,{(0,0928)^2}\,.\,\,0,3572 \approx 0,0092\].
* Điểm ba lần bắn là 30 điểm, có 1 trường hợp là cả ba viên vòng 10: Xác suất bằng 0,0008.
Vậy xác suất cần tìm bằng: P1 + P2 + 0,0008 = 0,00494.
Lời giải
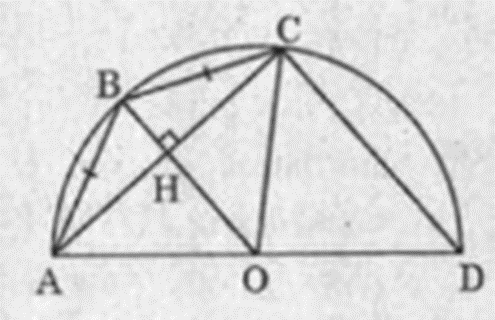
Dễ thấy OB là đường trung trực của AC nên \[OB \bot AC\] tại H và HA = HC
OH là đường trung bình của ∆ABC, ta có \[OH = \frac{1}{2}C{\rm{D}} = 3\]
• Xét ∆OHC vuông tại H, ta có:
HC2 = OC2 – OH2 = R2 – 9 (1)
• Xét ∆BHA vuông ở H, ta có:
HC2 = BC2 – BH2 = 20 – (R – 3)2 (2)
Từ (1) và (2) suy ra: R2 – 9 = 20 – (R – 3)2
⇔ R2 – 9 = 20 - R2 + 6R – 9
⇔ 2R2 – 6R – 20 = 0
⇔ (R – 5)(R + 2) = 0
⇔ R = 5 hoặc R = −2 (loại)
Vậy bán kính của đường tròn là 5 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
Nhắn tin Zalo