Câu hỏi:
12/07/2024 1,396
Cho hình bình hành ABCD, M và N lần lượt là trung điểm của AB và CD. Chứng minh các tứ giác AMCN là hình bình hành.
Cho hình bình hành ABCD, M và N lần lượt là trung điểm của AB và CD. Chứng minh các tứ giác AMCN là hình bình hành.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
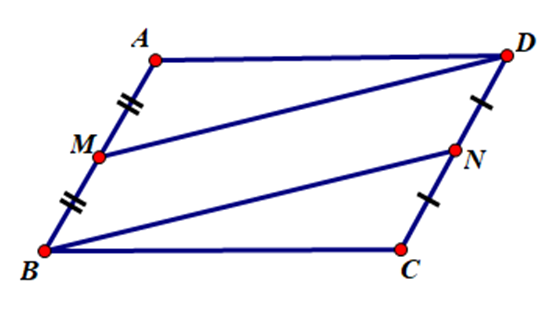
M là trung điểm của AB nên \[AM = MB = \frac{1}{2}AB\]
N là trung điểm của CD nên \[CN = ND = \frac{1}{2}CD\]
Vì ABCD là hình bình hành nên AB = CD và AB // CD
Suy ra \[\frac{1}{2}AB = \frac{1}{2}CD\]
Hay AM = CN và AM // CN
Suy ra AMCN là hình bình hành.
Vậy AMCN là hình bình hành.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Một người làm xong công việc hết số ngày là:
4 × 12 = 48 (ngày)
16 người làm xong công việc hết số ngày là:
48 : 16 = 3 (ngày)
Đáp số: 3 ngày.
Lời giải
Gọi số học sinh của ba lớp 7A, 7B, 7C lần lượt là x, y, z (học sinh) (x, y, z Î ℕ*)
Vì số học sinh của ba lớp 7A, 7B, 7C tỉ lệ với 21, 20, 22 nên:
\[\frac{x}{{21}} = \frac{y}{{20}} = \frac{z}{{22}}\]
Vì số học sinh lớp 7C nhiều hơn lớp 7A 2 học sinh nên: z – x = 2
Áp dụng dãy tỉ số bằng nhau ta có:
\[\frac{x}{{21}} = \frac{y}{{20}} = \frac{z}{{22}} = \frac{{z - x}}{{22 - 21}} = 2\]
Suy ra x = 21. 2 = 42 (tmđk), y = 20. 2 = 40 (tmđk), z = 22. 2 = 44 (tmđk)
Vậy số học sinh lớp 7A, 7B, 7C lần lượt là 42, 40, 44 học sinh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận