Câu hỏi:

14/06/2023 244

Cho tứ diện gần đều ABCD, biết AB = CD = 5, \(AD = BC = \sqrt {41} \). Tính sin góc giữa hai đường thẳng: B và CD.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

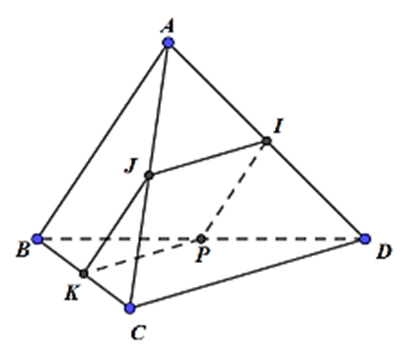
Cho tứ diện gần đều ABCD, biết AB = CD = 5, AD = BC = căn bậc hai 41. Tính sin góc (ảnh 1)

Gọi I, J, K, P lần lượt là trung điểm của AD, AC, BC, BD

Khi đó, AB // IP // JK, CD // IJ // KP

\( \Rightarrow \left( {\widehat {AB;\;CD}} \right) = \left( {\widehat {IP;\;KP}} \right)\)

Ta có: \(KP = \frac{1}{2}CD = \frac{5}{2};\;IP = \frac{1}{2}AB = \frac{5}{2}\)

\(A{K^2} = \frac{{A{B^2} + A{C^2}}}{2} - \frac{{B{C^2}}}{4} = \frac{{25 + 34}}{2} - \frac{{41}}{4} = \frac{{77}}{4} = D{K^2}\)

Tam giác AKD cân tại K có KI là trung tuyến

Þ KI ^ AD \( \Rightarrow I{K^2} = A{K^2} - A{I^2} = \frac{{77}}{4} - \frac{{41}}{4} = 9\)

\(\cos \widehat {IPK} = \frac{{I{P^2} + K{P^2} - I{K^2}}}{{2IP\,.\,KP}} = \frac{{\frac{{25}}{4} + \frac{{25}}{4} - 9}}{{2\,.\,\frac{5}{2}\,.\,\frac{5}{2}}} = \frac{7}{{25}} > 0\)

\( \Rightarrow \widehat {IPK} < 90^\circ \)

\( \Rightarrow \left( {\widehat {AB;\;CD}} \right) = \left( {\widehat {IP;\;KP}} \right) = \widehat {IPK}\)

\( \Rightarrow \sin \left( {\widehat {AB;\;CD}} \right) = \sin \widehat {IPK} = \sqrt {1 - {{\left( {\frac{7}{{25}}} \right)}^2}} = \frac{{24}}{{25}}\)

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình bình hành ABCD với AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE, MF cắt BC tại N.

a) Tứ giác MNCD là hình gì?

b) Tam giác EMC là tam giác gì?

c) Chứng minh: \(\widehat {BAD} = 2\widehat {AEM}\).

Xem đáp án

Lời giải

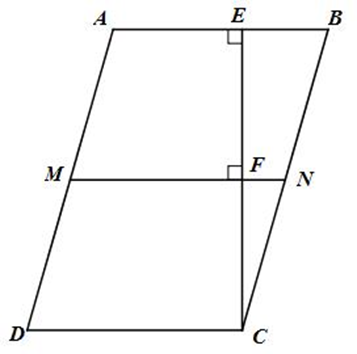
Cho hình bình hành ABCD với AD  2AB. Từ C vẽ CE vuông góc với AB. Nối E với (ảnh 1)

a) Ta có MN ^ CE (gt); AB ^ CE (gt)

Þ MN // AB

Mà AB // CD (ABCD là hình bình hành) nên MN // CD

Tứ giác MNCD có MN // CD

Và MD // CN (AD // BC, M Î AD, N Î BC)

Do đó tứ giác MNCD là hình bình hành.

b) Gọi F là giao điểm của MN và EC

Hình thang AECD (EC // CD) có MF // AE // CD

Và M là trung điểm của AD (gt)

Þ F là trung điểm của EC.

ΔMEC có MF là đường trung tuyến (F là trung điểm của EC)

Và MF là đường cao (MF ^ EC)

Þ ΔMEC cân tại M.

c) Ta có AD = 2AB (gt)

AD = 2MD (M là trung điểm của AD)

Và AB = CD (ABCD là hình bình hành) Þ MD = CD

Hình bình hành MNCD có MD = CD nên là hình thoi.

Þ CM là đường phân giác \(\widehat {EMF} = \widehat {CMF}\)

Mà \(\widehat {EMF} = \widehat {AEM}\) (hai góc so le trong và AE // MF)

Và \(\widehat {CMF} = \widehat {MCD}\) (hai góc so le trong và MF // CD)

Nên \(\widehat {AEM} = \widehat {MCD}\).

Ta có \(\widehat {AEM} = \widehat {MCD};\;2\widehat {MCD} = \widehat {NCD}\) (CM là tia phân giác của \(\widehat {NCD}\))

Và \(\widehat {NCD} = \widehat {BAD}\) (ABCD là hình bình hành)

\( \Rightarrow 2\widehat {AEM} = \widehat {BAD}\).

Câu 2

Cho các chữ số 1, 3, 4, 7, 8. Từ năm chữ số này có thể lập được tất cả bao nhiêu số chẵn có năm chữ số khác nhau?

Xem đáp án

Lời giải

Chữ số có năm chữ số cần tìm có dạng: \(\overline {abcde} \)

Vì số cần tìm là số chẵn nên e có 2 cách chọn: 4, 8

Chọn chữ số a có 4 cách chọn

Chọn chữ số b có 3 cách chọn

Chọn chữ số c có 2 cách chọn

Chọn chữ số d có 1 cách chọn

Vậy có tất cả 2.4.3.2.1 = 48 số có thể lập được

Câu 3