Câu hỏi:
11/07/2024 998
Cho hình thang ABCD, O là giao điểm của 2 đường chéo, đáy lớn CD. Đường thẳng qua A song song với BC cắt BD ở E và đường thẳng qua B song song với AD cắt đường thẳng AC tại F.
a) Chứng minh: EF // AB.
b) Chứng minh: AB2 = EF . CD.
Cho hình thang ABCD, O là giao điểm của 2 đường chéo, đáy lớn CD. Đường thẳng qua A song song với BC cắt BD ở E và đường thẳng qua B song song với AD cắt đường thẳng AC tại F.
a) Chứng minh: EF // AB.
b) Chứng minh: AB2 = EF . CD.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
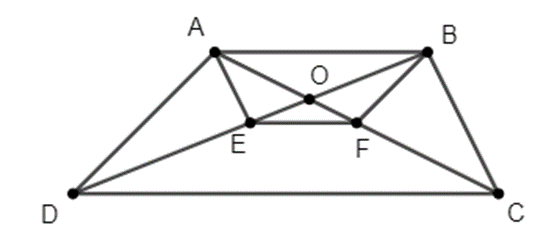
a) DO AE // BC nên áp dụng hệ quả định lí Ta-let, ta có:
\(\frac{{OE}}{{OB}} = \frac{{AO}}{{OC}}\)
Tương tự ta có: BF // AD
\(\frac{{OF}}{{OA}} = \frac{{OB}}{{OD}}\)
Mà AB // CD nên \(\frac{{OB}}{{OD}} = \frac{{OA}}{{OC}}\)
Từ đó suy ra \(\frac{{OF}}{{OA}} = \frac{{OE}}{{OB}} \Rightarrow \)EF // AB (đpcm).
b) Do AB // EF nên \(\frac{{EF}}{{AB}} = \frac{{OE}}{{OB}}\)
Do AB // CD nên \(\frac{{OA}}{{OC}} = \frac{{AB}}{{CD}}\)
Mà theo a) ta có: \(\frac{{OE}}{{OB}} = \frac{{AO}}{{OC}}\)
Nên \(\frac{{EF}}{{AB}} = \frac{{AB}}{{CD}}\)
Vậy AB2 = EF.CD (đpcm)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Nửa chu vi hình chữ nhật là: 40 : 2 = 20 (m)
Chiều dài của hình chữ nhật là:
(20 + 4) : 2 = 12 (m)
Chiều rộng của hình chữ nhật là:
20 – 12 = 8 (m)
Vậy diện tích của hình chữ nhật là:
12.8 = 96 (m2)
Đáp số: 96 m2.
Lời giải
• \(M = \frac{{{{100}^{100}} + 1}}{{{{100}^{99}} + 1}}\)\( = \frac{{{{100}^{100}} + 100 - 99}}{{{{100}^{99}} + 1}}\)
\( = \frac{{100({{100}^{99}} + 1) - 99}}{{{{100}^{99}} + 1}} = 100 - \frac{{99}}{{{{100}^{99}} + 1}}\).
• \(N = \frac{{{{100}^{101}} + 1}}{{{{100}^{100}} + 1}}\)\( = \frac{{{{100}^{101}} + 100 - 99}}{{{{100}^{100}} + 1}}\)
\( = \frac{{100({{100}^{100}} + 1) - 99}}{{{{100}^{100}} + 1}} = 100 - \frac{{99}}{{{{100}^{100}} + 1}}\)
Ta có: \(\frac{{99}}{{{{100}^{99}} + 1}} > \frac{{99}}{{{{100}^{100}} + 1}}\).
Do đó M < N.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo