Cho tam giác ABC vuông tại A. Đường cao AH. Kẻ phân giác của cắt AH tại M, kẻ phân giác của cắt BH tại N. Chứng minh rằng MN // AB.
Cho tam giác ABC vuông tại A. Đường cao AH. Kẻ phân giác của cắt AH tại M, kẻ phân giác của cắt BH tại N. Chứng minh rằng MN // AB.
Quảng cáo
Trả lời:
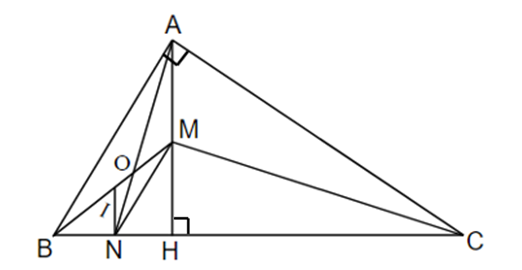
Áp dụng định lý đường phân giác trong tam giác ta có:
Xét ΔAHB và ΔCHA có:
AH chung
(cùng phụ với )
Do đó ΔAHB ᔕ ΔCHA (g.g)
Suy ra
Do đó,
Suy ra MN // AB (định lý Ta-let đảo)
Vậy MN // AB.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Áp dụng công thức ta có:
Vậy tỉ số truyền ở đây là: .
Vậy chi tiết đĩa líp quay nhanh hơn đĩa xích 4 lần.
Lời giải
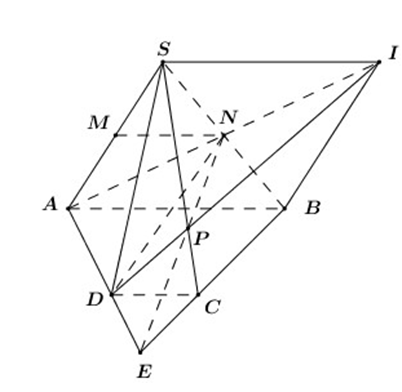
Trong (ABCD) gọi AD Ç BC = {E}
Ta có:
• E Î AD Ì (ADN) Þ E Î (ADN)
• E Î BC Ì (SBC) Þ E Î (SBC)
Do đó E Î (ADN) Ç (SBC)
Þ (ADN) Ç (SBC) = EN
Gọi SC Ç EN = {P}
Ta có: P Î SC
P Î EN Ì (ADN)
Þ P = SC Ç (ADN)
Vậy điểm P cần tìm là giao điểm của SC và ENLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.