Chứng minh rằng có vô số bộ ba số tự nhiên (a, b, c) sao cho a, b, c nguyên tố cùng nhau và số n = a2b2 + b2c2 + c2a2 là số chính phương.
Chứng minh rằng có vô số bộ ba số tự nhiên (a, b, c) sao cho a, b, c nguyên tố cùng nhau và số n = a2b2 + b2c2 + c2a2 là số chính phương.
Quảng cáo
Trả lời:
Giả sử a, b, c là ba số tự nhiên lẻ liên tiếp có dạng a = 2k – 1, b = 2k + 1, c = 2k + 3, với k ∈ ℕ.
Khi đó bộ ba số tự nhiên (a, b, c) nguyên tố cùng nhau.
Ta có n = a2b2 + b2c2 + c2a2
= (2k – 1)2(2k + 1)2 + (2k + 1)2(2k + 3)2 + (2k + 3)2(2k – 1)2
= (4k2 – 1)2 + (2k + 3)2.[(2k + 1)2 + (2k – 1)2]
= 16k4 – 8k2 + 1 + (4k2 + 12k + 9).[(2k + 1 + 2k – 1)2 – 2(2k + 1)(2k – 1)]
= 16k4 – 8k2 + 1 + (4k2 + 12k + 9).[16k2 – 2(4k2 – 1)]
= 16k4 – 8k2 + 1 + (4k2 + 12k + 9).(8k2 + 2)
= 16k4 – 8k2 + 1 + 32k4 + 8k2 + 96k3 + 24k + 72k2 + 18
= 48k4 + 96k3 + 72k2 + 24k + 18 + 1.
Ta có 48; 96; 72; 24; 18 đều chia hết cho 3.
Suy ra 48k4; 96k3; 72k2; 24k; 18 đều chia hết cho 3, với k ∈ ℕ.
Khi đó tổng 48k4 + 96k3 + 72k2 + 24k + 18 chia hết cho 3, với k ∈ ℕ.
Vì vậy 48k4 + 96k3 + 72k2 + 24k + 18 + 1 chia cho 3 dư 1, với k ∈ ℕ.
Suy ra n là số chính phương.
Vậy ta có điều phải chứng minh.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
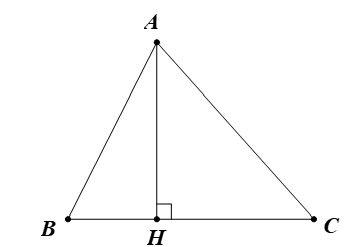
Giả sử ta cần vẽ hình chiếu của một điểm A trên cạnh BC, ta kẻ một đường thẳng đi qua điểm A và vuông góc với BC, đường thẳng này cắt BC tại H.
Vậy H là hình chiếu của một điểm A trên cạnh BC.
Câu 2
Lời giải
Dùng biểu đồ Ven, ta có:
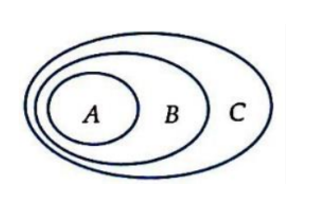
Ta thấy A ⊂ B ⇒ C \ B ⊂ C \ A.
Suy ra phương án B sai.
Vậy ta chọn phương án B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.