Cho đường tròn (O; R) và điểm A sao cho OA = 2R. Vẽ tiếp tuyến AB; AC với (O) (B, C là tiếp điểm).
a) Chứng minh tam giác ABC đều.
b) Đường vuông góc với OB tại O cắt AC tại D. Đường vuông góc với OC tại O cắt AB tại E. Chứng minh tứ giác ADOE là hình thoi.
Cho đường tròn (O; R) và điểm A sao cho OA = 2R. Vẽ tiếp tuyến AB; AC với (O) (B, C là tiếp điểm).
a) Chứng minh tam giác ABC đều.
b) Đường vuông góc với OB tại O cắt AC tại D. Đường vuông góc với OC tại O cắt AB tại E. Chứng minh tứ giác ADOE là hình thoi.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
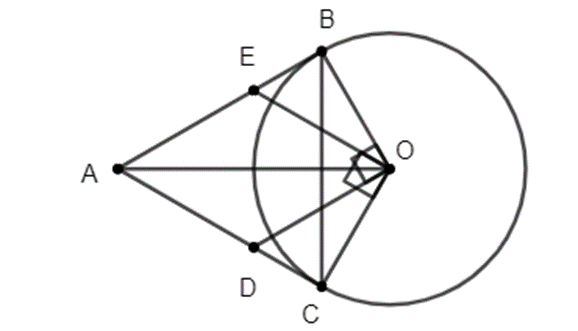
a) Ta có ∆AOC vuông tại C
\(\sin \widehat {CAO} = \frac{{OC}}{{OA}} = \frac{R}{{2R}} = \frac{1}{2} \Rightarrow \widehat {CAO} = 30^\circ \)
Mà A là giao điểm của 2 tiếp tuyến của (O).
\( \Rightarrow \widehat {BAC} = 2.\widehat {OAC} = 2.30^\circ = 60^\circ \) (1)
Và BA = AC (2)
Từ (1) và (2) nên ta có: ∆ABC đều.
b) Ta có: OD⊥OB; AB⊥OB
Suy ra OD // AB hay OD // AE (3)
Chứng minh tương tự: OE / /AD (4)
Từ (3), (4) suy ra ADOE là hình bình hành.
Ta có ∆AOC vuông tại C nên \(\widehat {OAB} + \widehat {AOB} = 90^\circ \)
\( \Rightarrow \widehat {AOB} = 90^\circ - \widehat {OAB} = 90^\circ - 30^\circ = 60^\circ \)
Ta lại có \(\widehat {DOB} = 90^\circ \Rightarrow \widehat {DOA} + \widehat {AOB} = 90^\circ \)
\( \Leftrightarrow \widehat {DOA} + 60^\circ = 90^\circ \Leftrightarrow \widehat {DOA} = 30^\circ \)
\( \Rightarrow \widehat {OAD} = \widehat {DOA} = 30^\circ \)
⇒ ∆DOA cân tại D
⇒ AD = DO.
Mà ADOE là hình bình hành nên ADOE là hình thoi.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
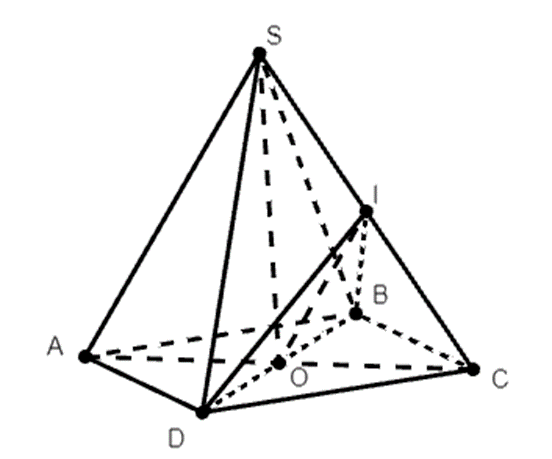
Ta có: IO//SA ⇒ IO//(SAD) và IO//(SAB) nên đáp án A và đáp án C đúng.
Ta có (SAC) ∩ (IBD) = IO nên đáp án D đúng.
Câu B ta có thiết diện là ∆IBD nên B sai.
Lời giải
Chọn 5 học sinh tùy ý trong 11 học sinh có số cách là: \(C_{11}^5\)
\( \Rightarrow n\left( \Omega \right) = 462\)
Gọi A là biến cố chọn ra 5 học sinh trong đó có cả nam và nữ.
Khi đó \(\overline A \) là biến cố chọn ra 5 học sinh trong đó tất cả là nữ hoặc tất cả là nam.
Suy ra n(\(\overline A \)) = \(C_6^5 + C_5^5 = 6 + 1 = 7\) (Cách)
\( \Rightarrow n(A) = n\left( \Omega \right) - n\left( {\overline A } \right) = 462 - 7 = 455\) (cách)
Vậy có 455 cách chọn ra 5 học sinh trong đó có cả nữ và nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.