Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Ta có: \(\overline {ab} \) + a + b = 95
⇔ a ´ 10 + b + a + b = 95
⇔ 11a + 2b = 95
⇔ aa + 2b = 95
Vì 95 là số lẻ , 2b là số chẵn nên aa là số lẻ.
Khi đó ta có: aa = {11; 33; 55; 77}
Để b là số có 1 chữ số thì 2b cao nhất là: 9 ´ 2 = 18
Ta có:
2b = 95 – 11 = 84 (loại)
2b = 95 – 33 = 62 (loại)
2b = 95 – 55 = 40 (loại)
2b = 95 – 77 = 18 (thỏa mãn)
Vậy số cần tìm là 79.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
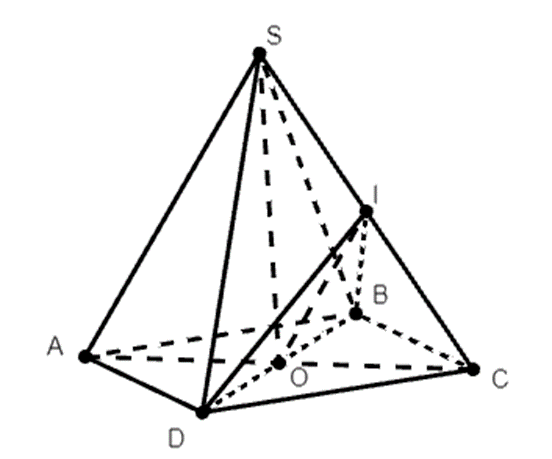
Ta có: IO//SA ⇒ IO//(SAD) và IO//(SAB) nên đáp án A và đáp án C đúng.
Ta có (SAC) ∩ (IBD) = IO nên đáp án D đúng.
Câu B ta có thiết diện là ∆IBD nên B sai.
Lời giải
Chọn 5 học sinh tùy ý trong 11 học sinh có số cách là: \(C_{11}^5\)
\( \Rightarrow n\left( \Omega \right) = 462\)
Gọi A là biến cố chọn ra 5 học sinh trong đó có cả nam và nữ.
Khi đó \(\overline A \) là biến cố chọn ra 5 học sinh trong đó tất cả là nữ hoặc tất cả là nam.
Suy ra n(\(\overline A \)) = \(C_6^5 + C_5^5 = 6 + 1 = 7\) (Cách)
\( \Rightarrow n(A) = n\left( \Omega \right) - n\left( {\overline A } \right) = 462 - 7 = 455\) (cách)
Vậy có 455 cách chọn ra 5 học sinh trong đó có cả nữ và nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.