Cho biểu thức: \(A = \frac{{{x^3} + 2{x^2} + x}}{{{x^3} - x}}\) (x ∉ {0; 1; −1})
a) Rút gọn biểu thức.
b) Tìm x để biểu thức A = 2.
c) Tìm giá trị nguyên của x để giá trị của biểu thức là một số nguyên.
Cho biểu thức: \(A = \frac{{{x^3} + 2{x^2} + x}}{{{x^3} - x}}\) (x ∉ {0; 1; −1})
a) Rút gọn biểu thức.
b) Tìm x để biểu thức A = 2.
c) Tìm giá trị nguyên của x để giá trị của biểu thức là một số nguyên.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Điều kiện x ≠ 0; x ≠ 1; x ≠ −1
a) Với x ≠ 0; x ≠ 1; x ≠ −1, ta có:
\(A = \frac{{{x^3} + 2{x^2} + x}}{{{x^3} - x}}\)
\( = \frac{{x({x^2} + 2x + 1)}}{{x\left( {{x^2} - 1} \right)}}\)
\( = \frac{{{{\left( {x + 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{x + 1}}{{x - 1}}\)
b) Với x ≠ 0; x ≠ 1; x ≠ −1, ta có:
\(A = \frac{{x + 1}}{{x - 1}} = 2\)
⇔ x + 1 = 2x – 2
⇔ x = 3 (TMĐK)
Vậy với x = 3 thì A = 2.
c) \(A = \frac{{x + 1}}{{x - 1}} = \frac{{(x - 1) + 2}}{{x - 1}} = 1 + \frac{2}{{x - 1}}\)
Để A nguyên thì 2 \( \vdots \) (x – 1)
⇒ (x – 1) ∈ Ư(2)
Mà Ư(2) = {1; −1; 2; −2}
⇒ x ∈ {2; 0; 3; −1}
Kết hợp với điều kiện x ≠ 0; x ≠ 1; x ≠ −1 ta có: x ∈ {2; 3}.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
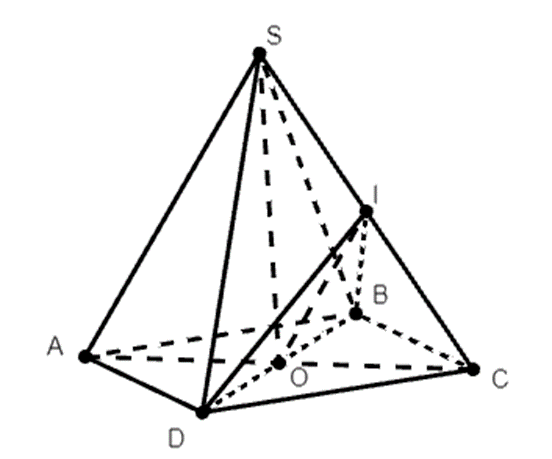
Ta có: IO//SA ⇒ IO//(SAD) và IO//(SAB) nên đáp án A và đáp án C đúng.
Ta có (SAC) ∩ (IBD) = IO nên đáp án D đúng.
Câu B ta có thiết diện là ∆IBD nên B sai.
Lời giải
Chọn 5 học sinh tùy ý trong 11 học sinh có số cách là: \(C_{11}^5\)
\( \Rightarrow n\left( \Omega \right) = 462\)
Gọi A là biến cố chọn ra 5 học sinh trong đó có cả nam và nữ.
Khi đó \(\overline A \) là biến cố chọn ra 5 học sinh trong đó tất cả là nữ hoặc tất cả là nam.
Suy ra n(\(\overline A \)) = \(C_6^5 + C_5^5 = 6 + 1 = 7\) (Cách)
\( \Rightarrow n(A) = n\left( \Omega \right) - n\left( {\overline A } \right) = 462 - 7 = 455\) (cách)
Vậy có 455 cách chọn ra 5 học sinh trong đó có cả nữ và nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.