Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, trung tuyến AM. Kẻ MD vuông góc với AB và Me vuông góc với AC.
a) Tứ giác ADME là hình gì? Vì sao?
b) Tìm điều kiện của tam giác ABC để tứ giác ADME là hình vuông.
c) Tính độ dài AM?
d) Tính diện tích tam giác ABM?
Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, trung tuyến AM. Kẻ MD vuông góc với AB và Me vuông góc với AC.
a) Tứ giác ADME là hình gì? Vì sao?
b) Tìm điều kiện của tam giác ABC để tứ giác ADME là hình vuông.
c) Tính độ dài AM?
d) Tính diện tích tam giác ABM?
Quảng cáo
Trả lời:
Lời giải
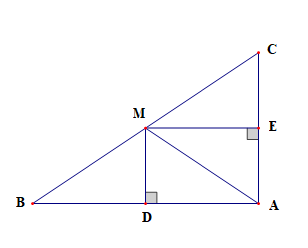
a) Vì MD ⊥ AB, ME ⊥ AC nên \(\widehat {M{\rm{D}}A} = \widehat {ME{\rm{A}}} = 90^\circ \)
Xét tứ giác ADME có \(\widehat {BAC} = \widehat {M{\rm{D}}A} = \widehat {ME{\rm{A}}} = 90^\circ \)
Suy ra ADME là hình chữ nhật
b) Để hình chữ nhật ADME là hình vuông thì AM là tia phân giác của \(\widehat {DA{\rm{E}}}\)
Khi đó tam giác ABC có AM vừa là phân giác vừa là trung tuyến
Nên tam giác ABC cân tại A
Vậy tam giác ABC vuông cân tại A thì ADME là hình vuông
c) Vì tam giác ABC vuông tại A, theo định lý Pytago ta có
BC2 = AB2 + AC2 = 82 + 62 = 100
Suy ra BC = 10 (cm)
Do đó \(AM = \frac{1}{2}BC = \frac{1}{2}.10 = 5\) (cm)
d) Vì MD ⊥ AB, AB ⊥ AC nên MD // AC (quan hệ từ vuông góc đến song song)
Xét tam giác ABC có M là trung điểm của BC và MD // AC
Suy ra MD là đường trung bình
Do đó \(M{\rm{D}} = \frac{1}{2}AC\)
Ta có: \(\frac{{{S_{ABM}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}M{\rm{D}}.AB}}{{\frac{1}{2}AC.AB}} = \frac{{M{\rm{D}}}}{{AC}} = \frac{1}{2}\)
Mà \[{{\rm{S}}_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.8.6 = 24\] (cm2)
Suy ra SABM = 12 cm2
Vậy SABM = 12 cm2.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
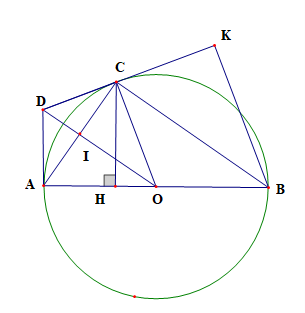
a) Xét tam giác ABC có O, I lần lượt là trung điểm của AB, AC
Suy ra OI là đường trung bình
Do đó OI // BC
b) Vì C thuộc đường tròn đường kính AB nên tam giác ABC nội tiếp (O)
Suy ra tam giác ABC vuông tại C
Xét (O) có AC là dây cung; I là trung điểm của AC
Suy ra OI là trung trực của AC
Mà D ∈ OI nên DA = DC
Xét ∆ADO và ∆CDO có
DA = DC (chứng minh trên)
DO là cạnh chung
OA = OC
Suy ra ∆ADO = ∆CDO (c.c.c)
Do đó \(\widehat {A{\rm{D}}O} = \widehat {AC{\rm{O}}}\) (hai góc tương ứng)
Mà \(\widehat {AC{\rm{O}}} = 90^\circ \) nên \(\widehat {A{\rm{D}}O} = 90^\circ \), hay AO ⊥ AD
Mà AO là bán kính của (O)
Do đó DA là tiếp tuyến của đường tròn tâm O
c) Ta có CO ⊥ CD, BK ⊥ CD
Suy ra CO // BK (quan hệ từ vuông góc đến song song)
Do đó \(\widehat {OCB} = \widehat {CBK}\) (hai góc so le trong)
Mà \(\widehat {CBO} = \widehat {OCB}\) nên \(\widehat {CBO} = \widehat {CKB}\)
Xét ∆BCH và ∆BCK có
\(\widehat {BHC} = \widehat {BKC}\left( { = 90^\circ } \right)\);
BC là cạnh chung;
\(\widehat {CBO} = \widehat {CKB}\) (chứng minh trên)
Suy ra ∆BCH = ∆BCK (cạnh huyền – góc nhọn)
Do đó CH = CK
Xét tam giác ABC vuông tại C có CH ⊥ AB, theo hệ thức lượng trong tam giác vuông ta có CH2 = HA . HB
Suy ra CK2 = HA . HB.
Lời giải
Lời giải
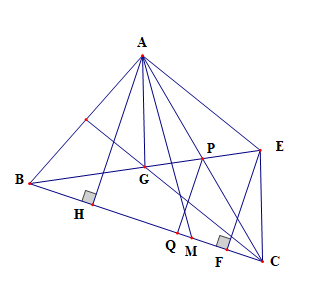
Dựng hình bình hành AGCE
Ta có \(\overrightarrow {MA} + \overrightarrow {GC} = \overrightarrow {MA} + \overrightarrow {A{\rm{E}}} = \overrightarrow {ME} \)
Kẻ EF ⊥ BC (F ∈ BC)
Khi đó \(\left| {\overrightarrow {MA} + \overrightarrow {GC} } \right| = \left| {\overrightarrow {ME} = ME} \right| \ge EF\)
Do đó \(\left| {\overrightarrow {MA} + \overrightarrow {GC} } \right|\) đạt giá trị nhỏ nhất khi M ≡ F
Gọi P là trung điểm của AC, Q là hình chiếu vuông góc của P lên BC
Vì AGCE là hình bình hành, P là trung điểm của AC
Suy ra P là trung điểm của GE
Do đó \(GP = PE = \frac{1}{2}GE\)
Vì G là trọng tâm tam giác ABC, BP là trung tuyến
Suy ra \(BG = \frac{2}{3}BP,GP = \frac{1}{3}BP\)
Ta có: BE = BP + PE
Hay \(BE = BP + \frac{1}{3}BP = \frac{4}{3}BP\)
Xét ∆BPQ và ∆BEF có
\(\widehat {FBE}\) là góc chung;
\(\widehat {BQP} = \widehat {BF{\rm{E}}}\left( { = 90^\circ } \right)\)
Suy ra (g.g)
Do đó \(\frac{{BP}}{{BE}} = \frac{{BQ}}{{BF}} = \frac{3}{4}\)
Hay \(\overrightarrow {BF} = \frac{4}{3}\overrightarrow {BQ} \)
Xét DAHC có P là trung điểm của AC và AH // PQ (vì cùng vuông góc với BC)
Suy ra Q là trung điểm của CH
Hay \(\overrightarrow {HQ} = \frac{1}{2}\overrightarrow {HC} \)
Mà \(\overrightarrow {BH} = \frac{1}{3}\overrightarrow {HC} \)
Ta có \(\overrightarrow {BQ} = \overrightarrow {BH} + \overrightarrow {HQ} = \frac{1}{3}\overrightarrow {HC} + \frac{1}{2}\overrightarrow {HC} = \frac{5}{6}\overrightarrow {HC} = \frac{5}{6}.\frac{3}{4}\overrightarrow {BC} = \frac{5}{8}\overrightarrow {BC} \)
Do đó \(\overrightarrow {BF} = \frac{4}{3}\overrightarrow {BQ} = \frac{5}{6}\overrightarrow {BC} \)
Vậy \[{\rm{x}} = \frac{5}{6}\] thì độ dài của \(\overrightarrow {MA} + \overrightarrow {GC} \) đạt giá trị nhỏ nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.