Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo M,N là trung điểm của OD và OB. Gọi E là giao điểm của AM và CD. F là giao điểm của CN và AB. Chứng minh: Tứ giác AMCN là hình bình hành.

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

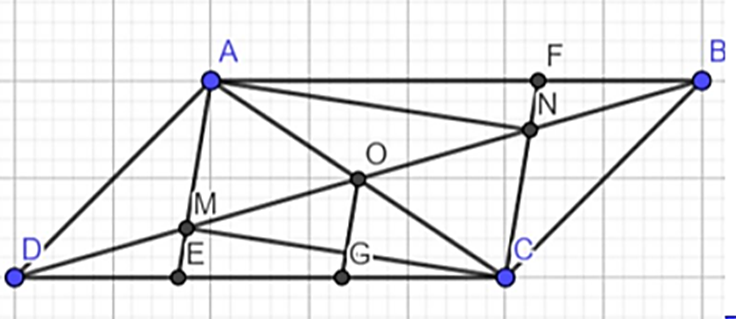
Ta có ABCD là hình bình hành

Þ AC Ç BD tại trung điểm của mỗi đường

Mà AC Ç BD = O

Þ O là trung điểm AC, DB

Lại có M, N là trung điểm OD, OB

\[ \Rightarrow OM = \frac{1}{2}OD = \frac{1}{2}OB = ON\]

Þ O là trung điểm MN

Do O là trung điểm của AC, MN

Þ AMCN là hình bình hành

Vậy AMCN là hình bình hành.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xem đáp án

Lời giải

Ta có: sin x + cos x = m

⇔ (sin x + cos x)² = m²

⇔ sin²x + 2sin x.cos x + cos²x = m²

⇔ (sin²x + cos² x) + 2sin x.cos x = m²

⇔ 1 + 2sin x.cos x = m²

\[ \Leftrightarrow \sin x.\cos x = \frac{{{m^2} - 1}}{2}\]

\[ \Rightarrow M = \frac{{{m^2} - 1}}{2}\]

Vậy \[M = \frac{{{m^2} - 1}}{2}\].

Câu 2

Xem đáp án

Lời giải

A ∪ B: tập hợp các học sinh hoặc học lớp 10 hoặc học môn Tiếng Anh của trường em.

A ∩ B: tập hợp các học sinh lớp 10 học môn Tiếng Anh của trường em.

A \ B: tập hợp các học sinh học lớp 10 nhưng không học môn Tiếng Anh của trường em.

B \ A: tập hợp các học sinh học môn Tiếng Anh của trường em nhưng không học lớp 10 của trường em.

Câu 3