Câu hỏi:
12/07/2024 981
Cho hình thang cân ABCD, đáy nhỏ CD = a, tổng hai góc \[\widehat A;\widehat B\] bằng nửa tổng hai góc \[\widehat C;\widehat D\], đường chéo AC vuông góc với hai cạnh bên BC. Tính các góc hình thang ABCD.
Cho hình thang cân ABCD, đáy nhỏ CD = a, tổng hai góc \[\widehat A;\widehat B\] bằng nửa tổng hai góc \[\widehat C;\widehat D\], đường chéo AC vuông góc với hai cạnh bên BC. Tính các góc hình thang ABCD.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
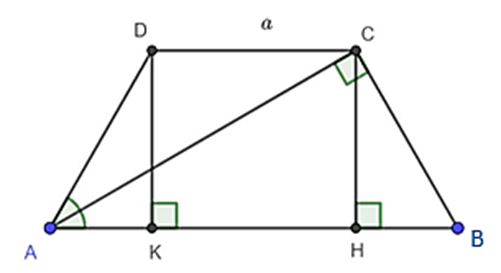
Theo đề ta có: \[\widehat A + \widehat B = \frac{1}{2}\left( {\widehat C + \widehat D} \right)\]
\[ \Rightarrow 2\widehat B = \frac{1}{2} \cdot 2\widehat C\] (do ABCD là hình thang cân) (1)
Mà \[\widehat B + \widehat C = 180^\circ \] (hai góc ở vị trí trong cùng phía) (2)
Từ (1) và (2) suy ra \[\widehat B + 2\widehat B = 180^\circ \]
\[ \Rightarrow \widehat B = 60^\circ \]
\[ \Rightarrow \widehat C = 120^\circ \]
Vậy \[\widehat A = \widehat B = 60^\circ \]; \[\widehat C = \widehat D = 120^\circ \].
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho sin x + cos x = m. Tính theo m giá trị của M = sin x.cos x.
Cho sin x + cos x = m. Tính theo m giá trị của M = sin x.cos x.
Xem đáp án »
13/07/2024
28,540
Câu 2:
Cho A là tập hợp các học sinh lớp 10 đang học ở trường em và B là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Hãy diễn đạt bằng lời các tập hợp sau: A ∪ B; A ∩ B; A \ B; B \ A.
Cho A là tập hợp các học sinh lớp 10 đang học ở trường em và B là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Hãy diễn đạt bằng lời các tập hợp sau: A ∪ B; A ∩ B; A \ B; B \ A.
Xem đáp án »
13/07/2024
13,496
Câu 4:
Rút gọn biểu thức: \[A = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{2012}}}}\].
Rút gọn biểu thức: \[A = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{2012}}}}\].
Xem đáp án »
13/07/2024
5,204
Câu 6:
Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh giỏi Toán và Lý, 5 học sinh giỏi Hoá và Lý, 4 học sinh giỏi Toán và Hoá, 3 học sinh giỏi cà 3 môn. Hỏi số học sinh giỏi ít nhất 1 môn trong 3 môn là bao nhiêu em?
Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh giỏi Toán và Lý, 5 học sinh giỏi Hoá và Lý, 4 học sinh giỏi Toán và Hoá, 3 học sinh giỏi cà 3 môn. Hỏi số học sinh giỏi ít nhất 1 môn trong 3 môn là bao nhiêu em?
Xem đáp án »
13/07/2024
4,511
Câu 7:
Chứng minh \[1 + tanx + ta{n^2}x + ta{n^3}x = \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}{{{{\cos }^3}x}}\].
Chứng minh \[1 + tanx + ta{n^2}x + ta{n^3}x = \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}{{{{\cos }^3}x}}\].
Xem đáp án »
13/07/2024
2,593
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận