Cho dãy số

1, \(\frac{1}{2},\,\frac{1}{4},\,\frac{1}{8},\,\,...\) (số hạng sau bằng một nửa số hạng liền trước nó).

Công thức tổng quát của dãy số đã cho là

A. \({u_n} = {\left( {\frac{1}{2}} \right)^n}\).

B. \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{{2^{n - 1}}}}\).

C. \({u_n} = \frac{1}{{2n}}\).

D. \({u_n} = {\left( {\frac{1}{2}} \right)^{n - 1}}\).

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 11 KNTT Bài tập cuối chương II có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

Đáp án đúng là: D

Xét từng đáp án, ta thấy:

+) Đáp án A, dãy số có số hạng tổng quát là \({u_n} = {\left( {\frac{1}{2}} \right)^n}\) có số hạng đầu \({u_1} = {\left( {\frac{1}{2}} \right)^1} = \frac{1}{2}\), không thỏa mãn.

+) Đáp án B, dãy số có số hạng tổng quát là \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{{2^{n - 1}}}}\) có số hạng đầu \({u_1} = \frac{{{{\left( { - 1} \right)}^1}}}{{{2^{1 - 1}}}} = - 1\), không thỏa mãn.

+) Đáp án C, dãy số có số hạng tổng quát là \({u_n} = \frac{1}{{2n}}\) có số hạng đầu \({u_1} = \frac{1}{{2.1}} = \frac{1}{2}\), không thỏa mãn.

+) Đáp án D, dãy số có số hạng tổng quát là \({u_n} = {\left( {\frac{1}{2}} \right)^{n - 1}}\) có số hạng đầu \({u_1} = {\left( {\frac{1}{2}} \right)^{1 - 1}} = 1\), thỏa mãn.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Hỏi sau 24 giờ, tế bào ban đầu sẽ phân chia thành bao nhiêu tế bào?

Xem đáp án

Lời giải

Lời giải:

Vì ban đầu có một tế bào và mỗi lần một tế bào phân chia thành hai tế bào nên ta có cấp số nhân với u₁ = 1, q = 2.

Vì cứ 20 phút lại phân đôi một lần nên sau 24 giờ sẽ có 24 . 60 : 20 = 72 lần phân chia tế bào và u₇₃ là số tế bào nhận đươc sau 24 giờ.

Vậy số tế bào nhận được sau 24 giờ phân chia là

u₇₃ = u₁ . q^{73 – 1} = 1 . 2^{73 – 1}= 2⁷² (tế bào).

Câu 2

Một hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1. Mỗi hình vuông màu vàng nhỏ hơn lại được chia thành chín hình vuông con, và mỗi hình vuông con ở chính giữa là được tô màu xanh. Nếu quá trình này được tiếp tục lặp lại năm lần, thì tổng diện tích các hình vuông được tô màu xanh bằng bao nhiêu?

Xem đáp án

Lời giải

Lời giải:

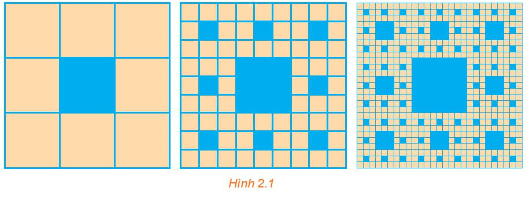
+ Chia lần 1: Hình vuông màu vàng lớn có cạnh bằng 1 đơn vị thì có diện tích bằng 1 (đvdt). Chia hình vuông này thành 9 hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh, thì hình vuông màu xanh đầu tiên này có diện tích bằng \(\frac{1}{9}\) (đvdt).

+ Chia lần 2: 8 hình vuông màu vàng còn lại, mỗi hình vuông này lại được chia thành 9 hình vuông con và tiếp tục tô xanh hình vuông chính giữa, khi đó mỗi hình vuông xanh nhỏ hơn có diện tích S₁ = \(\frac{1}{9} \cdot \frac{1}{9} = \frac{1}{{{9^2}}}\), 8 hình vuông xanh nhỏ hơn có diện tích bằng 8S₁.

Cứ tiếp tục như vậy, mỗi lần chia ta sẽ tạo thành 8 hình vuông xanh nhỏ hơn tiếp đối với mỗi ô vuông vàng nhỏ.

Do đó, quá trình này được tiếp tục lặp lại năm lần, thì trừ lần đầu tiên, 4 lần sau, mỗi lần chia diện tích ô vuông xanh tạo thành lập thành một cấp số nhân có u₁ = \(8.\frac{1}{{{9^2}}}\) và công bội \(q = 8.\frac{1}{9}\).

Vậy tổng diện tích các hình vuông được tô màu xanh là

S = \(\frac{1}{9} + \frac{{8.\frac{1}{{{9^2}}}\left( {1 - {{\left( {\frac{8}{9}} \right)}^4}} \right)}}{{1 - \frac{8}{9}}} = \frac{{26\,\,281}}{{59\,\,049}}\) (đvdt).

Câu 3