Câu hỏi:
13/07/2024 3,443
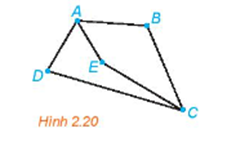
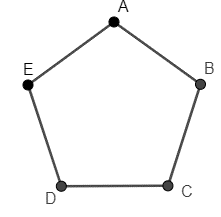
Có 5 thành phố du lịch A, B, C, D, E và các con đường nối các thành phố này như Hình 2.20. Hãy chỉ ra một cách để đi tham quan cả 5 thành phố đó, mà không cần đến địa điểm nào quá một lần.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
Một cách để đi tham quan cả 5 thành phố đó, mà không cần đến địa điểm nào quá một lần là ta có thể đi theo thứ tự EABCD (hoặc có thể chọn ECBAD, hoặc BADCE,...).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
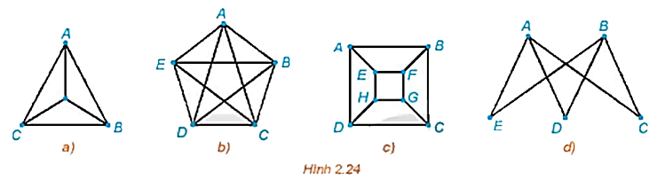
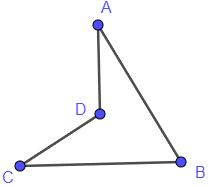
+) Đồ thị Hình 2.24 a) có các đỉnh đều có bậc là 3 nên theo định lí Euler đồ thị này không có chu trình Euler.
Lại có đồ thị a) có 4 đỉnh, tổng số bậc của hai đỉnh không kề nhau luôn không nhỏ hơn 4 nên theo định lí Ore, đồ thị a) có một chu trình Hamilton.
Một chu trình Hamiltol của đồ thị a) là ABCDA.
+) Đồ thị Hình 2.24 b) liên thông và có các đỉnh đều có bậc chẵn (ở đây là bậc 4) nên theo định lí Euler, đồ thị này có một chu trình Euler. Một chu trình Euler của đồ thị này là ABCDEADBECA.
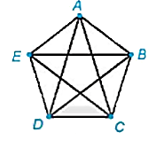
Lại có đồ thị b) có 5 đỉnh, tổng số bậc của hai đỉnh không kề nhau luôn không nhỏ hơn 5 nên theo định lí Ore, đồ thị b) có một chu trình Hamilton.
Một chu trình Halminton của đồ thị này là ABCDEA.
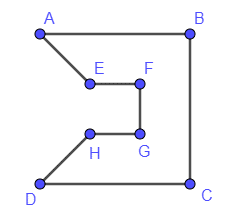
+) Đồ thị Hình 2.24 c) có các đỉnh đều có bậc là 3 nên theo định lí Euler đồ thị này không có chu trình Euler.
Lại có đồ thị c) có 8 đỉnh, mặc dù đồ thị này không thỏa mãn cả 2 định lí Ore và Dirac nhưng đồ thị vẫn có một chu trình Hamilton.
Một chu trình Hamiltol của đồ thị c) là ABCDHGFEA.
+) Đồ thị Hình 2.24 d) có đỉnh A và B là đỉnh bậc 3, nên theo định lí Euler đồ thị này không có chu trình Euler. Đồ thị d) này cũng không có chu trình Hamilton.
Lời giải
Lời giải:
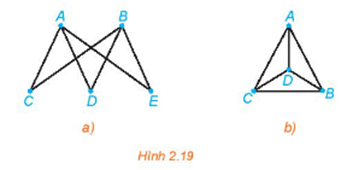
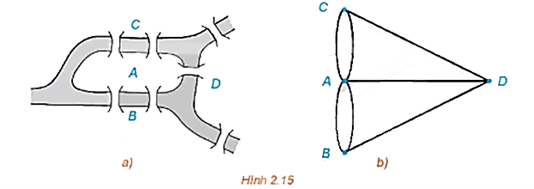
- Đồ thị Hình 2.19a có đường đi Euler từ A đến B vì đồ thị này liên thông và các đỉnh A, B có bậc 3 (bậc lẻ), còn các đỉnh C, D, E đều có bậc 2 (bậc chẵn). Một đường đi Euler của đồ thị này là ACBDAEB.
- Đồ thị Hình 2.19b không có đường đi Euler vì đồ thị này có bốn đỉnh bậc lẻ (ở đây là bậc bằng 3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
33 câu trắc nghiệm Toán 11 Kết nối tri thức Bài 29: Công thức cộng xác suất có đáp án
-
10 Bài tập Biểu diễn góc lượng giác trên đường tròn lượng giác (có lời giải)